우도와 확률 이론 | Likelihood and Probability Theory

---

KEYWORDS
Likelihood, Likelihood란, 가능도, 우도, 우도란, 베이즈 정리, 가우시안 분포, 빈도론, 베이지안, 조건부 분포

---

     

확률 이론 ^{Probability Theory}

• 측정 노이즈(Measurement Noise)는 오류나 환경 요인으로 인해 데이터에 발생하는 변동을 의미합니다.
  • 데이터셋이 유한한 크기를 가질 경우 기저 패턴에 대한 불완전한 정보가 생깁니다.
  • 확률 이론(Probability Theory)은 이러한 불확실성을 이해하고 정량화하기 위한 방법으로, 보다 정확한 예측을 가능하게 합니다.
  • 의사결정 이론 (Decision Theory)과 결합하면, 불완전한 정보를 바탕으로 최적의 예측을 하는 데 도움이 됩니다.
• ex. 서로 다른 양의 과일이 담긴 빨간 상자와 파란 상자
  • 무작위로 상자를 선택하고 과일을 관찰하는 과정은 확률론적으로 모델링될 수 있으며, 이를 통해 확률의 기초 개념을 이해할 수 있습니다.

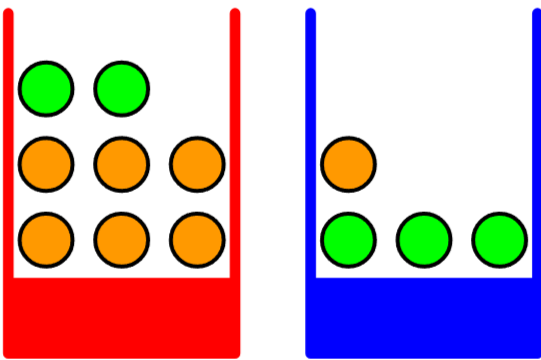Simple example of two coloured boxes ¹

• 확률 변수(Random Variables)

  • 상자의 정체(빨간 상자 또는 파란 상자)는 확률 변수 \(B\)로 표기합니다.
    • 가능한 값: \(B = r\) (빨간 상자) 또는 \(B = b\) (파란 상자)
  • 과일의 정체(사과 또는 오렌지)는 확률 변수 \(F\)로 표기합니다.
    • 가능한 값: \(F = a\) (사과) 또는 \(F = o\) (오렌지)

• 확률의 정의(Probability Definition)

  • 확률(Probability)은 전체 시행 횟수 중 사건이 발생하는 비율로 정의되며, 시행 횟수가 무한에 가까워질수록 수렴하는 값입니다.
  • 예를 들어, 10번 중 4번 빨간 상자를 선택했다면 확률은 다음과 같이 표현됩니다:
  \[p(B = r) = \frac{4}{10}\]

  • 마찬가지로, 파란 상자의 경우:

    \[p(B = b) = \frac{6}{10}\]

     

확률의 성질과 규칙

• 확률의 성질(Properties of Probabilities)

  • 확률은 \(0\)에서 \(1\) 사이의 값을 갖습니다. 상호 배타적이며 모든 가능한 결과를 포함하는 사건들에 대해, 확률의 합은 1이 됩니다.
  \[p(B = r) + p(B = b) = 1\]

• 기본 확률 규칙(Basic Probability Rules)

  • 확률의 두 가지 기본 규칙인 합의 법칙(Sum Rule)과 곱의 법칙(Product Rule)을 살펴봅니다.
  • 합의 법칙 (Sum Rule) ㅣ 사건 \(X\)의 확률은 \(Y\)의 모든 가능한 값에 대해 \(X\)와 \(Y\)의 결합 확률을 합산하여 구할 수 있습니다:
    • 여기서 \(p(X)\)는 \(X\)의 주변 확률(Marginal Probability)을 나타냅니다.
    • \(p(X, Y)\)는 \(X\)와 \(Y\)의 결합 확률(Joint Probability)입니다.
  \[p(X) = \sum_Y p(X, Y)\]
  • 곱의 법칙(Product Rule) ㅣ 두 사건 \(X\)와 \(Y\)의 결합 확률은 조건부 확률과 연결됩니다:
    • \(p(Y ㅣ X)\)는 \(X\)가 발생했을 때 \(Y\)가 발생할 조건부 확률입니다.
    • 이는 \(X\)를 알고 있을 때 \(Y\)의 확률을 결정하는 데 도움이 됨을 강조합니다.
  \[p(X, Y) = p(Y | X) p(X)\]

     

베이즈 정리 ^{Bayes’ Theorem}

• 베이즈 정리(Bayes' Theorem)
  • 아래 수식으로 알려진 베이즈 정리(Bayes’ Theorem)는 조건부 확률 간의 관계를 보여주며, 패턴 인식과 머신러닝 분야에서 중요한 역할을 합니다.

\[p(Y | X) = \frac{p(X | Y) p(Y)}{p(X)}\]

• 핵심 용어
  • 결합 확률 \(p(X, Y)\) (Joint Probability) ㅣ 사건 \(X\)와 \(Y\)가 동시에 발생할 확률입니다.
  • 조건부 확률 \(p(Y ㅣ X)\) (Conditional Probability) ㅣ 사건 \(X\)가 발생했을 때 사건 \(Y\)가 발생할 확률입니다.
  • 주변 확률 \(p(X)\) (Marginal Probability) ㅣ \(Y\)와 관계없이 사건 \(X\)가 발생할 확률입니다.

• 베이즈 정리 이해하기
  • 베이즈 정리에서 좌변 \(p(Y ㅣ X)\)는 우리가 계산하고자 하는 조건부 확률입니다.
  • 우변은 다음으로 구성됩니다:
    • \(p(XㅣY)\) ㅣ \(Y\)가 주어졌을 때 \(X\)의 조건부 확률
    • \(p(Y)\) ㅣ \(Y\)의 사전 확률(Prior Probability)
    • \(p(X)\) ㅣ 정규화 상수 역할을 하는 \(X\)의 전체 확률

  • 정규화(Normalization) ㅣ 아래 수식은 \(X\)의 확률을 구하기 위해 \(Y\)가 \(X\)에 기여하는 모든 가능한 방법을 고려해야 함을 나타냅니다.

    \[p(X) = \sum_Y p(X | Y) p(Y)\]

     

조건부 확률 ^{Conditional Probability}

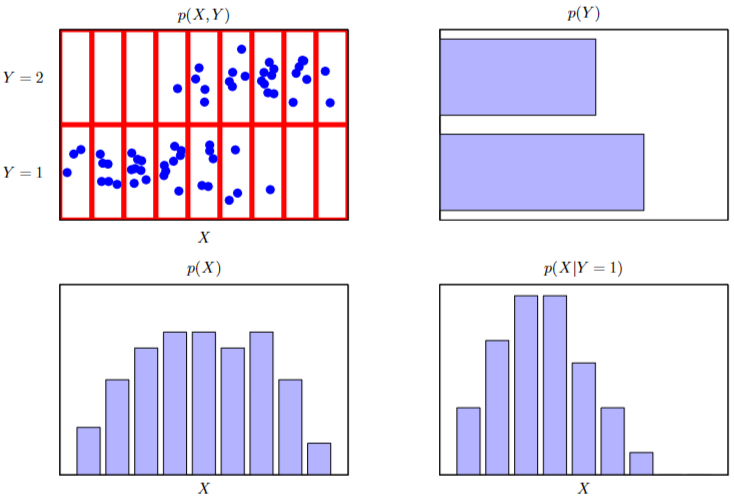An illustration of a distribution over two variables ¹

1. 상자 선택 확률 | Probability of Selecting Boxes

\[p(B = r) = \frac{4}{10} \\ p(B = b) = \frac{6}{10}\]

• 이 확률들은 다음 조건을 만족합니다:

\[p(B = r) + p(B = b) = 1\]

2. 과일 유형에 대한 조건부 확률 | Conditional Probabilities for Fruit Types

• 파란 상자가 선택되었을 때, 사과를 선택할 확률은 다음과 같습니다:

\[p(F = a | B = b) = \frac{3}{4}\]

• 선택된 상자에 따른 과일 유형의 확률은 다음과 같습니다.

빨간 상자의 경우:

\[p(F = a | B = r) = \frac{1}{4}\] \[p(F = o | B = r) = \frac{3}{4}\]

파란 상자의 경우:

\[p(F = a | B = b) = \frac{3}{4}\] \[p(F = o | B = b) = \frac{1}{4}\]

• 이 조건부 확률들도 정규화되어 있음을 주목해야 합니다:

\[p(F = a | B = r) + p(F = o | B = r) = 1\] \[p(F = a | B = b) + p(F = o | B = b) = 1\]

3. 전체 확률 계산: 합의 법칙과 곱의 법칙 적용 | Calculating Overall Probability

• 사과를 선택할 전체 확률은 다음과 같이 계산됩니다:

\[p(F = a) = p(F = a | B = r) p(B = r) + p(F = a | B = b) p(B = b)\] \[= \frac{1}{4} \times \frac{4}{10} + \frac{3}{4} \times \frac{6}{10} = \frac{11}{20}\]

• 이후 합의 법칙을 이용하면:

\[p(F = o) = 1 - p(F = a) = 1 - \frac{11}{20} = \frac{9}{20}\]

4. 베이즈 정리 적용: 역조건부 확률 | Applying Bayes’ Theorem

• 오렌지가 선택되었을 때, 그것이 빨간 상자에서 왔을 확률을 계산합니다:

\[p(B = r | F = o) = \frac{p(F = o | B = r) p(B = r)}{p(F = o)}\] \[= \frac{\frac{3}{4} \times \frac{4}{10}}{\frac{9}{20}} = \frac{2}{3}\]

• 결과적으로, 파란 상자의 확률은:

\[p(B = b | F = o) = 1 - p(B = r | F = o) = 1 - \frac{2}{3} = \frac{1}{3}\]

5. 사전 확률과 사후 확률: 해석 | Prior and Posterior Probabilities

• 확률 \(p(B)\)는 과일의 정체를 관찰하기 전의 사전 확률(Prior Probability)을 나타냅니다.
• \(p(BㅣF)\)는 선택된 과일이 오렌지임을 관찰한 후의 사후 확률(Posterior Probability)로, 갱신된 믿음을 나타냅니다.
• 이는 특정 결과를 관찰하면 사전 믿음이 크게 영향받을 수 있음을 보여줍니다. 과일 유형이 알려지면 빨간 상자의 가능성이 높아지는 것이 그 예입니다.

6. 변수의 독립성: 독립 개념 | Independence of Variables

• 두 확률 변수 \(X\)와 \(Y\)가 \(p(X, Y) = p(X) p(Y)\)를 만족하는 결합 분포를 가지면 독립(Independent)입니다.
• 과일 상자 예제에서, 두 상자 모두 사과와 오렌지의 비율이 같다면 \(p(F ㅣ B) = p(F)\)임을 의미하여, 상자 선택이 사과를 선택할 가능성에 영향을 미치지 않습니다.

     

베이지안 확률 ^{Bayesian Probability}

• 빈도론 vs. 베이지안(Frequentist vs. Bayesian)
  • 빈도론적(Frequentist) 해석은 반복 가능한 사건의 빈도를 기반으로 확률을 정의합니다.
  • 베이지안(Bayesian) 해석은 불확실성을 정량화하며, 새로운 증거를 통해 불확실한 사건에 대한 믿음을 갱신할 수 있습니다.
• 불확실성의 예시(Example of Uncertainty)
  • 북극 빙하의 용해나 달의 역사적 궤도와 같은 사건은 반복될 수 없지만, 결과에 대한 믿음의 정도로 논의할 수 있습니다.
  • 새로운 증거는 믿음의 수정을 이끌며, 이는 과학적·실용적 맥락의 의사결정에 필수적입니다.
• 콕스의 공리(Cox’s Axioms)
  • Cox(1946)는 믿음의 정도에 수치를 사용한다면, 그 수치가 확률의 규칙을 따라야 함을 보여주는 공리 집합을 제시했습니다.
  • 이는 확률이 불확실성을 포함하는 영역으로 부울 논리를 확장할 수 있음을 보여줍니다.
• 패턴 인식에 적용 하기
  • 다항식 곡선 피팅과 같은 패턴 인식 맥락에서, 빈도론적 개념은 무작위 관측을 이해하는 데 도움이 되고, 베이지안 확률은 모델 파라미터의 불확실성을 명확히 표현하고 정량화하는 데 도움이 됩니다.

     

베이즈 정리 (베이지안 관점)

• 베이지안 해석(Bayesian Interpretation)

  • 베이즈 정리는 새로운 증거를 바탕으로 특정 가설의 확률을 조정하는 데 도움이 됩니다.

  • 모델 파라미터 \(w\)에 대한 사전 믿음을, 데이터(아래와 같이 표기)를 관측한 후의 사후 확률로 변환합니다: \(D = \{t_1, \ldots, t_N\}\)

• 사전 확률과 우도(Prior and Likelihood)

  • 데이터를 관측하기 전, 파라미터 \(w\)에 대한 가정은 사전 확률 분포 \(p(w)\) (Prior Probability Distribution)에 담깁니다. 데이터를 관측한 후, 우도 함수 \(p(Dㅣw)\) (Likelihood Function)는 파라미터 \(w\)의 각 값에 대해 관측된 데이터가 얼마나 가능성이 있는지를 설명합니다.
• 베이즈 정리 공식(Bayes’ Theorem Formula)
  • 이 수식은 사후 확률 \(p(wㅣD)\)가 우도 \(p(Dㅣw)\)와 사전 확률 \(p(w)\)의 곱에 비례함을 보여줍니다.
  \[p(w|D) = \frac{p(D|w) \cdot p(w)}{p(D)}\]
• 정규화 상수(Normalization Constant)
  • 분모의 \(p(D)\)는 사후 분포가 1로 적분되도록 보장하는 정규화 상수로, 이를 통해 사후 분포가 유효한 확률 밀도로 인정받습니다.
• 패러다임별 우도(Likelihood in Different Paradigms)
  • 베이지안 통계학에서 우도 함수 \(p(Dㅣw)\)는 파라미터의 함수로 간주되며, \(w\)에 대한 확률 분포를 의미하지 않습니다.
  • 빈도론적 맥락에서는 \(w\)와 같은 파라미터가 고정되어 있다고 보고, 최대 우도 추정법 (Maximum Likelihood Estimation)을 사용하여 \(p(Dㅣw)\)를 최대화하는 파라미터 추정치를 찾습니다.
• 오류 함수(Error Function)
  • 머신러닝에서 우도 함수의 음의 로그는 오류 함수(Error Function)로 정의되며, 이를 통해 모델 파라미터를 반복적으로 조정하여 모델 성능을 향상시킵니다.

     

빈도론 vs. 베이지안 ^{Frequentist vs. Bayesian}

• 최대 우도 추정(Maximum Likelihood Estimation, MLE) - 빈도론적 관점
  • 주어진 데이터의 우도를 최대화하는 파라미터 값을 찾는 것에 중점을 둡니다.
  • 우도 함수 \(p(Dㅣw)\)는 파라미터 \(w\)가 주어졌을 때 데이터 \(D\)가 얼마나 가능성이 있는지를 나타냅니다.
  • 우도의 음의 로그를 머신러닝의 오류 함수로 사용하면, 우도 최대화가 음의 로그-우도 최소화와 동치임을 이용해 최적화를 수행할 수 있습니다.
• 부트스트랩 방법(Bootstrap Method)
  • 데이터를 복원 추출(Resampling with Replacement)하여 여러 데이터셋을 만들고, 각 데이터셋에서의 예측 변동을 평가하여 파라미터 추정의 정확성을 측정하는 빈도론적 기법입니다.
• 베이지안 관점(Bayesian Perspective)
  • 이 접근 방식은 사전 분포(Prior Distribution)를 통해 사전 지식을 자연스럽게 통합하며, 관측된 데이터에 따라 결론을 수정합니다.
  • 예를 들어, 동전이 세 번 앞면이 나왔다면, 베이지안 접근법은 앞면의 확률을 1로 주장하는 대신 더 온건한 추정값을 제공합니다.
• 패러다임 간 논쟁(Controversy Between Paradigms)
  • 빈도론과 베이지안 접근법은 그 장점에 대한 지속적인 논쟁이 있습니다.
  • 빈도론적 방법은 사전 확률 선택에 따른 편향으로부터 일정한 보호를 제공할 수 있고, 베이지안 방법은 마르코프 체인 몬테카를로(MCMC)와 변분 추론(Variational Inference)과 같은 계산 기술의 발전으로 더욱 주목받고 있습니다.

     

가우시안 분포 ^{Gaussian Distribution}

• 단일 변수 \(x\)에 대해 다음과 같이 수식으로 표현됩니다:

\[N(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left\{-\frac{1}{2\sigma^2} (x - \mu)^2\right\}\]

• 평균(Mean)은 분포의 중심이 어디에 위치하는지를 나타냅니다.
  • 분산(Variance)은 평균을 중심으로 값들이 얼마나 퍼져 있는지를 나타냅니다.
• 다차원 벡터 \(\mathbf{x}\)에 대해서는 다음과 같이 표현이 변합니다:

\[N(\mathbf{x}|\mu, \Sigma) = \frac{1}{(2\pi)^{D/2} |\Sigma|^{1/2}} \exp\left\{-\frac{1}{2} (\mathbf{x} - \mu)^T \Sigma^{-1} (\mathbf{x} - \mu)\right\}\]

• \(\mu\)는 \(\mathbf{x}\)의 차원에 해당하는 평균 벡터입니다.
  • \(\Sigma\)는 변수의 서로 다른 차원이 함께 변하는 방식(상관관계)을 포착하는 공분산 행렬(Covariance Matrix)입니다.
  • \(\vert \Sigma \vert\)는 공분산 행렬의 행렬식으로, 다차원 공간에서 분포의 부피에 대한 통찰을 제공합니다.
• 가우시안 분포는 데이터 분석과 이론의 다양한 영역에서 많은 응용을 보이며, 특히 여러 확률 변수의 합을 다룰 때 자주 등장합니다.

     

조건부 가우시안 분포 ^{Conditional Gaussian Distribution}

• 벡터 \(\mathbf{x}\)가 결합 가우시안 분포를 갖는 경우:

  \[N(\mathbf{x}|\mu, \Sigma)\]
  • 이 벡터를 두 부분집합 \(\mathbf{x}_a\)와 \(\mathbf{x}_b\)로 분리하면, 한 집합이 주어졌을 때 다른 집합의 조건부 분포도 가우시안 분포가 됩니다.

• 이 개념을 설명하는 핵심 수식은 다음과 같습니다:

\(\mathbf{x}\)를 부분집합 \(\mathbf{x}_a\)와 \(\mathbf{x}_b\)로 분리합니다:

\[\mathbf{x} = (\mathbf{x}_a, \mathbf{x}_b)\]

평균 벡터 \(\mu\)를 분리합니다:

\[\mu = (\mu_a, \mu_b)\]

공분산 행렬 \(\Sigma\)를 분리합니다:

\[\Sigma = \begin{pmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \end{pmatrix}\]

• 공분산 행렬의 역행렬인 정밀도 행렬 \(\Lambda\) (Precision Matrix)도 분리된 형태로 주어집니다:
  • 이 정밀도 행렬은 공분산보다 정밀도 관점에서 더 명확하게 정의되는 가우시안 분포의 특정 성질을 부각시키는 데 유용합니다.

\[\Lambda = \begin{pmatrix} \Lambda_{aa} & \Lambda_{ab} \\ \Lambda_{ba} & \Lambda_{bb} \end{pmatrix}\]

     

가우시안 변수에 대한 베이즈 정리 ^{Bayes’ Theorem for Gaussian Variables}

• 선형 가우시안 모델의 기초 가정은 변수 \(x\)에 대한 사전 \(x\)가 주어졌을 때의 관측 모델(우도)이 모두 가우시안이라는 점입니다.
• 주변 분포 \(p(x)\)는 다음과 같이 표기됩니다:
  • \(\mu\)는 평균이고, \(\Lambda\)는 정밀도 행렬입니다.

\[p(x) = N(x | \mu, \Lambda^{-1})\]

• 조건부 분포 \(p(yㅣx)\)는 다음과 같이 표현됩니다:

\[p(y|x) = N(y | Ax + b, L^{-1})\]

• \(A\)는 선형 관계를 나타내는 계수 행렬이고, \(b\)는 편향 항(Bias Term)입니다.
  • \(L\)은 관측 노이즈의 정밀도입니다.
• 이 가정 아래 결합 로그확률은 \(x\), \(y\)에 대한 이차식이 되고, 따라서 결합분포도 가우시안입니다.
  • 벡터 \(\mathbf{z}\)에 대한 결합 분포(아래)는 두 분포의 로그를 사용하여 공식화할 수 있습니다:

\[\mathbf{z} = \begin{pmatrix} x \\ y \end{pmatrix}\] \[\ln p(\mathbf{z}) = \ln p(x) + \ln p(y|x)\] \[= -\frac{1}{2}(x - \mu)^T \Lambda (x - \mu) - \frac{1}{2}(y - Ax - b)^T L(y - Ax - b) + \text{const}\]

• 관측 \(y\)를 얻었을 떄 \(x\)에 대한 사후분포는 닫힌 형태의 가우시안으로 주어집니다:

\[p(x\mid y) = N\!\big(x \mid \Sigma\{A^{T}L(y-b) + \Lambda\mu\},\; \Sigma\big)\]

• 여기서 사후 공분산 \(\Sigma\)는 다음과 같습니다:

\[\Sigma = (\Lambda + A^{T}LA)^{-1}.\]

• 사후 평균은 두 정보의 합성 결과로 이해할 수 있습니다.
  • 사전에서 오는 정보 \(\Lambda\mu\), 다른 하나는 관측으로부터 오는 정보 \(A^T L(y-b)\)이며, 이 둘이 정밀도 관점에서 합쳐져 사후 평균을 만듭니다.
  • 사후 공분산은 사전의 정밀도 \(\Lambda\)에 관측으로부터 얻는 정밀도 \(A^T L A\)가 더해진 형태의 역행렬이므로(정밀도가 증가), 사후 불확실성은 줄어듭니다.
  • 이 관계는 베이지안 관점에서 사전 + 데이터 \(\rightarrow\) 사후라는 직관을 정확하게 수학적으로 표현합니다.

     

주변 가우시안 분포와 조건부 가우시안 분포 ^{Marginal and Conditional Gaussians}

• 결합분포의 정밀도(Precision) 행렬은 다음과 같은 형태를 가집니다:

\[R = \begin{pmatrix} \Lambda + A^{T}LA & -A^{T}L \\ - L A & L \end{pmatrix}.\]

• 이 정밀도의 역행렬(결합 공분산)을 계산하면 다음과 같습니다:
  • 여기서 \(\mathbf{z} = \begin{pmatrix} x \\ y \end{pmatrix}\) 입니다.
  • 이 분할 공분산으로부터 주변분포와 조건부분포를 바로 읽을 수 있습니다.

\[\mathrm{cov}[\mathbf{z}] = R^{-1} = \begin{pmatrix} \Lambda^{-1} & \Lambda^{-1}A^{T} \\ A\Lambda^{-1} & L^{-1} + A\Lambda^{-1}A^{T} \end{pmatrix},\]

• 주변 분포 \(p(y)\)의 평균과 공분산은 다음과 같습니다:
  • 주변 평균은 선형변환된 사전 평균 \(A\mu\)에 편향 \(b\)를 더한 것이고, 주변 공분산은 두 성분의 합입니다.
  • 하나는 관측 노이즈의 공분산 \(L^{-1}\)이고, 다른 하나는 사전에서 투사된 불확실성 \(A \Lambda^{-1} A^T\)입니다.
  • 즉, 관측값 \(y\)의 변동성은 원래의 상태 불확실성과 관측 노이즈가 함께 기여한 결과입니다.

\[p(y) = N\big(y\mid A\mu + b,\; L^{-1} + A\Lambda^{-1}A^{T}\big).\]

• 조건부 분포 \(p(xㅣy)\)는 앞서의 베이지안 결과와 동일하게 닫힌형의 가우시안입니다.
  • 만약 \(A=I\)이면, 이는 두 가우시안의 합(합성, Convolution)에 해당하고, 이 경우 주변 평균은 두 평균의 합, 주변 공분산은 두 공분산의 합으로 간단히 해석됩니다.

\[p(x\mid y) = N\!\big(x \mid \Sigma\{A^{T}L(y-b) + \Lambda\mu\},\; \Sigma\big),\quad \Sigma = (\Lambda + A^{T}LA)^{-1}.\]

• 선형 가우시안 모델에서는 결합분포, 주변분포, 조건부분포가 모두 가우시안이고, 이들 사이의 관계는 정밀도/공분산의 덧셈과 행렬 역연산으로 깔끔하게 계산됩니다.
• 베이지안 관점에서의 사전 정밀도와 관측으로부터의 정밀도가 더해져 사후 정밀도가 형성되며, 사후 평균은 사전에 데이터로부터 오는 정보의 정밀도 가중 합으로 이해할 수 있습니다.

     

---

Reference

1. Bishop, Christopher M., and Nasser M. Nasrabadi. Pattern recognition and machine learning. Vol. 4. No. 4. New York: springer, 2006. ↩︎ ↩︎²