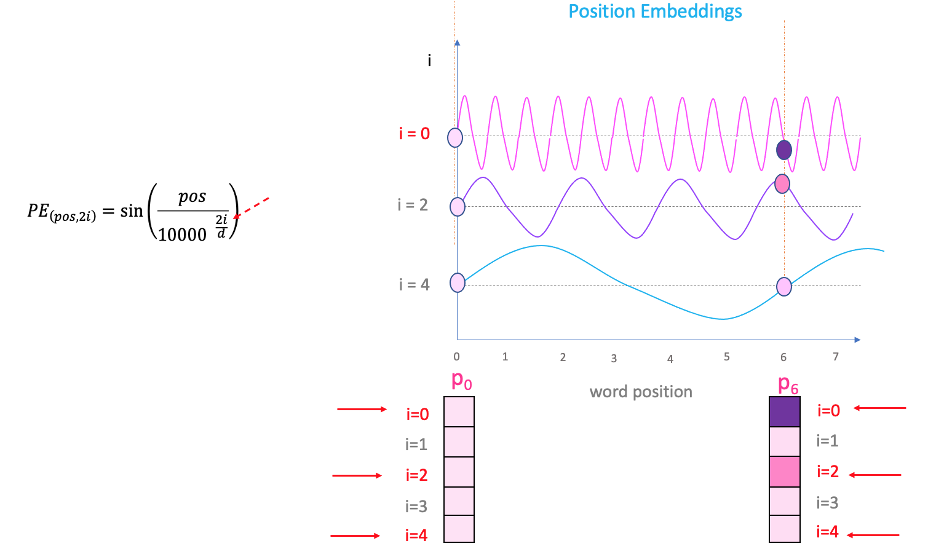
Positional Encoding 이해하기
Transformer 구조에 활용되는 Positional Encoding의 개념과 역할, 수식을 설명합니다.
Positional encoding은 Transformer 에서 사용되는 중요한 요소 중 하나입니다.
Transformer는 순차적인 구조를 사용하지 않기에 입력 시퀀스의 각 위치에 대한 정보를 인코딩하는 방법이 필요합니다.
따라서 Transformer에서는 입력 토큰의 위치 정보를 임베딩에 직접 추가하여 모델에게 위치 정보를 제공하는 Positional Encoding 방식을 활용합니다.
위치 임베딩 Positional Encoding 이란?
- Vision Transformer (ViT)에는 RNN과 다르게 단어의 순서라는 개념이 존재하지 않습니다.
- 따라서 각 단어 임베딩에 위치/순서에 대한 신호를 추가하여, 모델이 단어의 순서 정보를 함께 포함시킬 수 있도록 도와줍니다. 이를 Positional Encoding이라고 부릅니다.
- 이는 다음과 같은 조건을 만족해야 합니다.
- 각 time step (문장 내 단어의 위치) 에 대해 고유한 인코딩을 출력해야 합니다.
- 두 time step 사이의 거리는 문장의 길이와 상관없이 일관되어야 합니다.
- 값들은 문장의 길이와 상관없이 bounded 되어야 합니다.
- Positional Encoding은 위 기준들을 충족하면서, 위치 정보를 포함하는 벡터로 정의됩니다.
- 또한, 이 벡터는 모델 자체에 통합되지 않고 문장 내 각 단어의 위치에 대한 정보를 제공하는데 사용됩니다.
Positional Encoding Formulation
- DefinitionㅣPositional Encoding
- 위치(픽셀) \(pos \in [0, L-1]\) 와 단어 \(w\)에 대하여,
모델의 입력 벡터 차원 \(d_{\text{model}}=4\) 라고 할때 4차원 임베딩 \(e_w\) 에 대한 모델에 들어가는 임베딩 \(e'_{w}\) 는 다음과 같이 정의됩니다.
- 각 임베딩에 Positional Encoding을 더하기 위해 위치 임베딩의 차원을 단어 임베딩의 차원과 동일하게 유지합니다. \((d_{\text{word embedding}} =d_{\text{positional embedding}})\)
- 각 주파수에 대한 사인/코사인 함수들의 쌍으로 이해할 수 있습니다.
- \(10000\)은
Attention is all you need1 의 저자가 설정한 값입니다.
- 위치(픽셀) \(pos \in [0, L-1]\) 와 단어 \(w\)에 대하여,
- 일반화 하여 Positional encoding을 표현하면 아래와 같습니다. \(i\) 는 임베딩 차원의 인덱스를 의미합니다.
where \(d_{\text{model}}=512 \,\,\) (i.e., \(\,\, i \in [0,255]\)) in the original paper 2.
- \(d\)가 고정된 상태에서, \(pos\) 와 \(i\)는 아래와 같이 움직입니다.
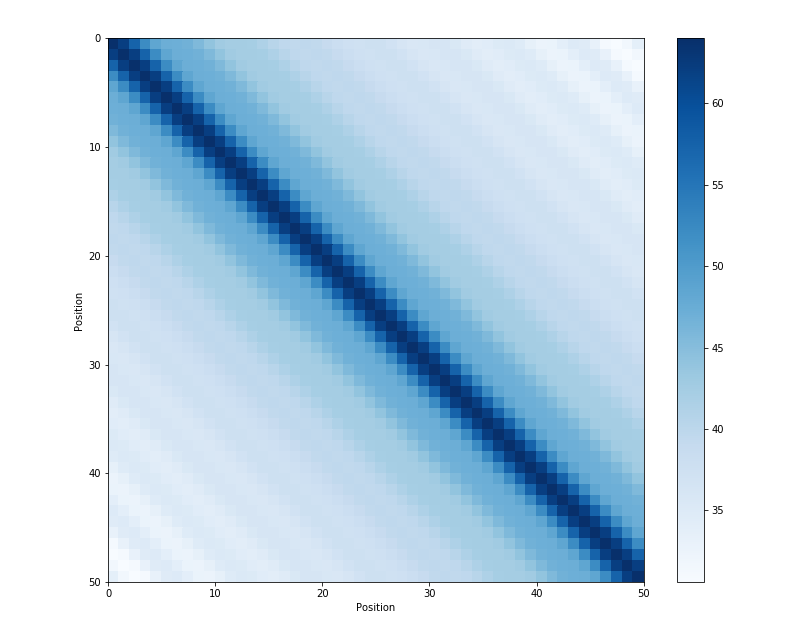
A sin curve and vary “pos” (on the x-axis) 3
- \(\frac{pos}{10000^{2i/d_{\text{model}}}}\)는 픽셀 또는 패치의 위치를 나타냅니다. 픽셀 또는 패치의 위치에 따라 \(sin(x)\) 와 \(cos(x)\) 의 값이 달라집니다.
- \(\frac{1}{10000^{2i/d}}\) 에 해당하는 주파수는 벡터 차원을 따라 감소하며 \(2 \pi\) 부터 \(10000 \times 2 \pi\) 파장의 기하학적인 수열을 생성합니다.
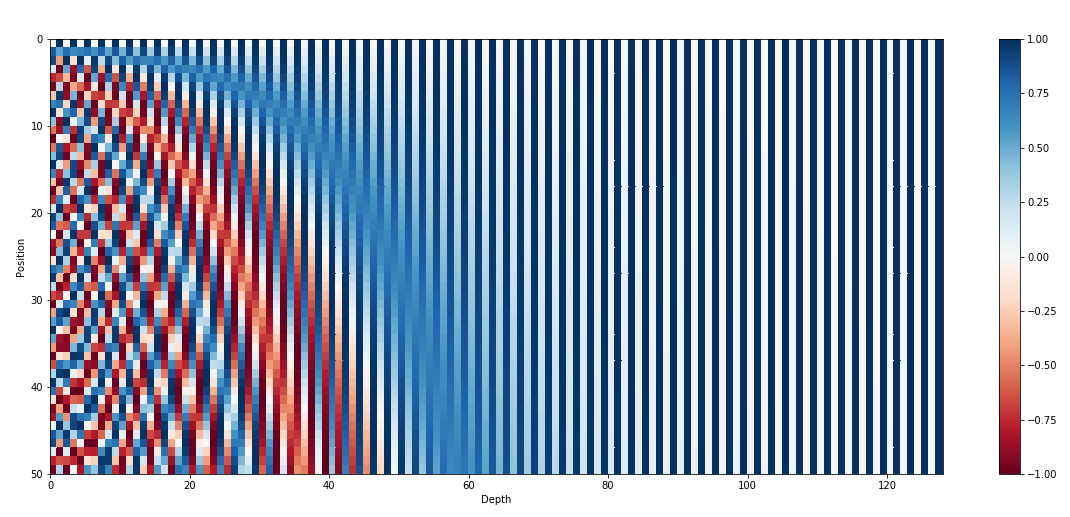The 128-dimensional positonal encoding for a sentence with the maximum lenght of 50 4
Positional Encoding 원리 이해하기
- Transformer는 입력 임베딩 각각에 위치 임베딩을 추가하여 각 단어의 위치 또는 시퀀스에 있는 여러 단어 사이의 거리를 결정하는 데 도움을 줍니다.
- 임베딩 벡터가 인코더 내 Q/K/V 벡터에 투영되고 내적 계산 중에 임베딩 벡터 사이에 의미 있는 거리를 결정합니다.
- 논문 3 에 의하면 Positional Encoding에 Sinusoidal Function을 활용하는 이유는 \(\text{PE}(pos, 2i+1)\)는 \(\text{PE}(pos, 2i)\)의 선형 함수로 표현될 수 있어, 모델이 상대 위치에 할당하는 방법을 쉽게 학습할 수 있기 때문입니다.
Theorem 주파수 \(w_i\) 에 대응하는 모든 sin, cos 쌍에 대하여, 아래의 식을 만족하는 선형 변환 \(M \in \mathbb{R}^{2 \times 2}\) 이 존재합니다.
\[M \cdot \begin{bmatrix} \sin(w_i \cdot t) \\ \cos(w_i \cdot t) \end{bmatrix} = \begin{bmatrix} \sin(w_i \cdot (t+\phi)) \\ \cos(w_i \cdot (t+\phi)) \end{bmatrix},\] \[M_{\phi, i} = \begin{bmatrix} \cos(w_i \cdot \phi) & \sin(w_i \cdot \phi) \\ -\sin(w_i \cdot \phi) & \cos(w_i \cdot \phi) \end{bmatrix}.\]또한 Sinusoidal Function은 인접한 time step 사이의 거리가 대칭 형태를 띈다는 특징을 가지며, 이는 시간에 따라 적절하게 감소합니다.
- 이러한 사인 및 코사인 함수는 주기적이기 때문에 시퀀스 길이에 상관없이 항상 동일한 범위 \([-1,1]\) 를 가집니다.
Positional Embedding 을 더하는 이유
- 위치 임베딩을 더하지 않고 연결 하려면 projection 에 대한 추가 매개변수들이 필요하며 이는 더 많은 메모리 사용을 야기합니다.
- 하지만 위 이유 외에도 더하는 것의 이점을 직관적으로 설명하는 의견 5이 있습니다.
- Attention에서는 두 단어 임베딩 \(x, y\) 을 각각 Query와 Key 행렬에 통과시키고, 결과 Query와 Key 벡터의 유사성을 내적으로 비교합니다.
- 위치 임베딩 \(e, f\) 을 단어 임베딩에 각각 추가함으로써 위 내적 과정이 변화하며, 단어 간의 위치 관계를 함께 고려할 수 있습니다.
- \(x' (Q'Ky)\)에 3개의 term이 추가된 형태입니다.
- 위치 임베딩과 함께 학습된 변환행렬 \(Q'K\)는 여러 작업을 동시에 수행해야 하지만 고차원에서 무작위로 선택된 벡터는 거의 항상 근사적으로 직교하기 때문에 효율적으로 이루어질 수 있습니다.
- 이 근사적 직교성은 두 부분 공간이 서로 독립적으로 변환될 수 있음을 의미하며, 이를 통해 위치와 단어의 특성을 거의 동시에 학습할 수 있게 됩니다.
한계점
- 픽셀 또는 패치의 위치에 따라 벡터의 크기가 달라집니다.
- \(d_{\text{model}}\) 이 커질수록 positional encoding의 벡터의 크기가 커집니다.
- 개선하기 위해 다음과 같은 방법이 제안되었습니다.
- Learned positional encoding: Positional encoding을 학습 가능한 벡터로 대체합니다.
- Relative positional encoding: 픽셀 또는 패치의 상대적인 위치 정보를 입력 데이터에 추가합니다.
References
This post is licensed under CC BY 4.0 by the author.