Softmax 함수 신뢰도와 딥러닝 예측의 불확실성 | Softmax Confidence and Uncertainty

Softmax Calibration의 개념을 소개하고 수학적 정의를 설명하며, 방법론의 설명과 실습 코드를 제공합니다.

최근 딥러닝 모델은 예측 시 과도한 확신을 가지는 경향이 있으며, 이는 모델의 신뢰도를 왜곡할 수 있다고 알려져 있습니다.

특히, Softmax 예측값은 실제 가능성을 정확히 반영하지 못해 Calibration 문제를 야기하며, 이는 자율주행차나 의료 진단 등에서 위험을 야기할 수 있습니다.

효과적인 Calibration 방법론으로는 Histogram Binning, Isotonic Regression, Platt Scaling 등이 있으며, 이를 통해 예측의 신뢰도를 향상시킬 수 있다.

     

Introduction

• 일반적으로 현대의 딥러닝 모델은 Over-confident하게 예측을 하는 경우가 많음 ^{1 2 3 4 5}
  • Overfitting 없이 학습된 모델이라도 예측을 할때는 너무 높은 확신을 가지는 경향이 있음.
  • 사용자의 입장에서 모델이 애매한 예측을 할 때, 낮은 Confidence (= 실제 Confidence, Calibrated Confidence) 를 부여해야 예측에 대한 해석이 용이함.
• 딥러닝 모델은 단순히 정답만 잘 맞출 뿐만 아니라, 실제 정답일 가능성을 정확히 알려줄 필요가 있음.
  • 보행자와 장애물을 감지해야하는 자율 주행 차의 경우, 장애물을 확실하게 감지하지 못할 때 낮은 Confidence를 부여한다면 다른 센서의 출력을 더 신뢰하여 정확한 브레이크 감속이 가능함.
  • AI를 이용한 암 진단의 경우, 암 여부가 확실하지 않을 때 낮은 Confidence를 부여해야만 의사가 재확인 하는 식으로 더 정확하게 의사 결정할 수 있음.

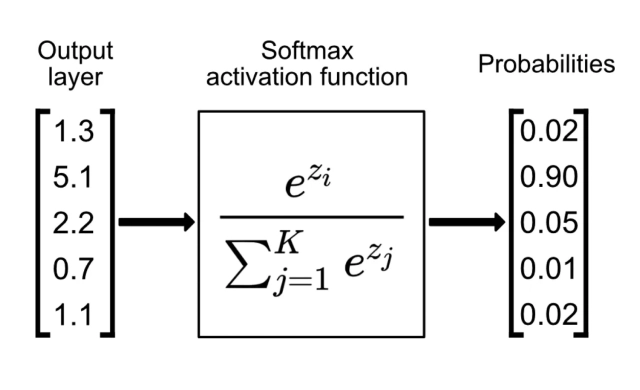Softmax activation function ⁶

     

Softmax 함수와 신뢰도 (Confidence)

• 분류 Task를 위한 딥러닝 모델의 경우 최종 출력으로 Softmax 활성화 함수를 사용함.

  • Softmax는 신경망 모델의 출력 $z_i$ 을 0과 1사이의 값으로 변환하여 각 클래스에 대한 확률로 해석할 수 있도록 함.

  • 이 중 가장 높은 확률 값을 가지는 클래스가 신경망의 예측 클래스이며, 해당 클래스에 대한 예측 확률을 신뢰도 (Confidence) 라 정의함.

  • Softmax 함수
    \(\sigma(z_i) = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_j}}.\)

• 하지만 Softmax 신뢰도를 있는 그대로 해석하기에는 몇 가지 한계가 있음.

     

Softmax 출력의 한계

1. Calibration 문제

• 현대의 딥러닝 모델은 예측에 과도하게 확신하는 경향이 있으며, 이는 Softmax 출력을 실제로 얼마나 신뢰할 수 있는지를 왜곡할 수 있음. ¹
• Softmax 출력이 0.9인 경우, 모델은 해당 예측에 대해 90% 신뢰도 (Confidence) 를 가진다고 해석할 수 있지만, 실제로 그 확신이 과장되었을 수 있음.
• 이는 모델이 충분히 Calibration 되지 않았기 때문임.

     

Calibration 이란?

• 신경망의 Output이 실제 정답 가능성 (Calibrated Confidence) 을 제대로 나타내는 문제
• Output이 실제 Confidence를 반영한다면, 아래의 예시 (Lenet 모델) 와 같이 Confidence와 Accuracy가 일치해야 함.

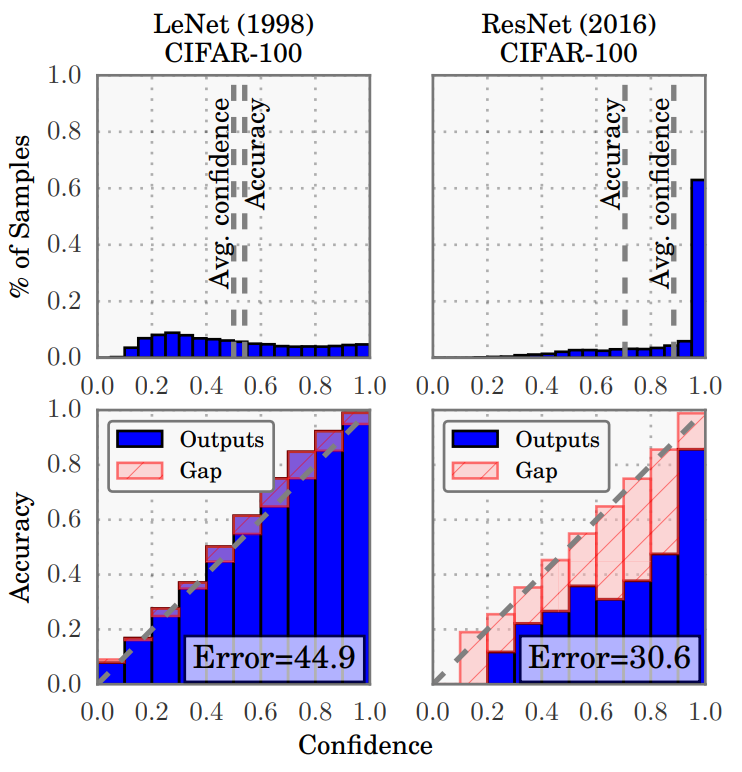Confidence histograms and reliability diagrams for Lenet and Resnet on Cifar100 ¹

Definition

• Multi-class classfication task 의 경우 입력변수를 아래와 같이 정의할 수 있음.

\[X \in \mathcal{X}, \quad Y \in \mathcal{Y} = \{ 1, ..., K \}, \quad \text{where $K$ is the number of classes.}\\\]

• 해당 입력 변수들은 Ground truth joint distribution을 따르는 무작위 변수임.
  \(\pi (X, Y) = \pi (Y | X) \pi (X).\)

• 신경망 모델을 아래와 같이 정의함. \(h(X) = (Y, P), \\ \text{where $\hat{Y}$ is a class prediction and $\hat{P}$ is its associated confidence (probability of correctness).}\)

Calibrated Confidence

• $\hat{P}$가 진정한 확률을 나타내도록 추정하는 것을 의미함.
• 100개의 예측이 있고 Confidence가 0.8이라면, 이 중 80개가 정확히 분류될 것으로 예상함.
• 연속적인 확률 값인 $\hat{P}$를 유한한 데이터로 계산하는 것은 불가능하므로 근사적으로 추정하는 것이 적절함.

\[P(\hat{Y} = Y | \hat{P} = p) = p, \quad \forall p \in [0,1].\]

• 과거의 신경망은 이진 분류 작업에서 일반적으로 Calibrated Confidence를 잘 생성하는 것으로 알려져 있었지만, 현대의 신경망은 성능에 비해 Calibration 능력이 떨어진다는 사실이 밝혀짐. ¹

     

Calibration에 영향을 주는 요소

모델 크기 ^{Model Capacity}

• 모델의 Depth와 Width가 증가함에 따라 모델의 크기가 증가하지만, 이는 Calibration에 부정적인 영향을 미침.

• 모델 학습 후 모델이 거의 모든 학습 데이터를 올바르게 분류할 수 있게 되면, Negative log likelihood (NLL)이 높아짐으로써 예측의 Confidence를 높일 수 있으나 모델은 점점 Over-confident 하게 됨.

  • Negative log likelihood (NLL)

    • Probabilistic model의 품질을 측정하는 표준 방법이며, 딥러닝에서는 Cross entropy loss로 알려져 있음. \(\mathcal{L} = - \sum^n_{i=1} \log (\hat{\pi}(y_i | x_i)).\)
    • NLL is minimized $\Longleftrightarrow$ \(\hat{\pi} (Y | X) \quad \text{recovers the ground truth conditional distribution} \quad \pi (Y|X).\)

• NLL은 간접적으로 모델의 Calibration 정도를 측정할 수 있으며, 신경망이 NLL에 Overfitting 될 수 있지만 0/1 손실 (정확도) 에는 Overfitting 되지 않을 수 있음.

  • NLL이 Overfitting 되는 현상은 분류 정확도에는 도움이 되지만, 잘 모델링된 확률에는 방해요소로 작용함.

• 모델 크기가 증가할 수록 Expected Calibration Error (ECE) 가 크게 증가함.

  • Expected Calibration Error (ECE) ⁷

    • 신경망의 예측이 얼마나 잘 Calibrated 되었는지 하나의 스칼라 값으로 나타내는 것
    • 모든 예측을 M개의 동일한 간격 bin으로 나누고, 각 bin에서 예측 정확도와 신뢰도의 차이에 대한 가중 평균을 계산함.
    \[ECE = \sum_{m=1}^M \frac{|B_m|}{n}|acc(B_m) - conf(B_m)|,\] \[acc(B_m) = \frac{1}{|B_m|} \sum_{i \in B_m} 1 (\hat{y_i} = y_i),\] \[conf(B_m) = \frac{1}{|B_m|} \sum_{i \in B_m} \hat{p}_i,\] \[\text{where $M$ is the number of bins, $B_m$ is the set of indexes with samples in m-th bin }\] \[\text{and $n$ is the number of all samples.}\\\]

배치 정규화 ^{Batch Normalization}

• 배치 정규화는 신경망 내 활성화 함수의 분포 변동을 최소화하여 최적화를 개선하고 정확도를 높이는 역할을 함.
• 하지만 경우에 따라 모델의 최종 예측에 부정적인 영향을 미칠 수 있음.
  • 배치 정규화가 적용된 모델의 Calibration 저하는 Learning rate와 같은 하이퍼 파라미터와는 무관하게 적용됨.

Weight Decay

• 현대의 신경망에는 Batch normalization의 규제 효과가 더 좋은 일반화 성능을 보이기에, Weight decay는 거의 사용되지 않음.
• 적은 Weight decay로 학습된 모델들은 Calibration에 부정적 영향을 미침.
  • 모델이 Over-regularization 또는 Under-regularization 모두를 보이더라도, 전체적인 General calibration은 Weight decay가 증가할 수록 향상됨.
  • 최적의 정확도 성능을 달성한 후에도 Weight decay가 추가되면 Calibration이 계속해서 개선됨.

     

Calibration 방법

• Post-processing calibration이며, 이를 위해 학습된 데이터 외 추가로 홀드아웃 검증 데이터셋이 필요함.
  • 검증 데이터셋은 Hyper-parameter 조정에도 사용될 수 있음.
• 학습, 검증, 테스트 데이터 모두 동일한 분포에서 나왔다고 가정함.

Histogram Binning ⁸

• Non-parametric 방식으로 예측된 확률을 여러 구간으로 나누고 각 구간에 Calibration을 더함.

• 모든 예측값 $\hat{p_i}$를 Mutually exclusive한 구간 $B_1, …, B_M$으로 나누고, 각 $B_m$에 점수 $\theta_m$을 할당함.
  • $\hat{p}_i$가 $B_m$에 속하면, Calibration이 적용된 예측값 $\hat{q}_i$는 $\theta_m$.
• 테스트 시 예측: 만약 $\hat{p}{te}$가 $B_m$에 속하면, Calibration이 적용된 예측값 $\hat{q}{te} = \theta_m$이 됨.
• 목표
  • Bin-wise 제곱 오차 최소화. 아래를 최소화하여 적절한 $\theta_m$을 선택함. \(\min_{\theta_1,...,\theta_M} \sum^M_{m=1}\sum^n_{i=1} 1 (a_m \leq \hat{p_i} < a_{m+1})(\theta_m - y_i)^2, \\\) \(\text{subject to $0 = a_1 \le a_2 \le ... \le a_{M+1} = 1, \quad \theta_1 \le \theta_2 \le ... \le \theta_M.$}\\\) \(\text{$M$ is the number of intervals; $a_1,...,a_{M+1}$ are the interval boundaries; }\) \(\text{and $\theta_1,...,\theta_M$ are the function values.}\)

Isotonic Regression ⁹

• 계단 함수 형태의 Non-parametric 방법이며, 예측값을 Calibration하기 위해 각 구간의 경계와 경계 내 예측값을 최적화 함.

• Histogram binning은 미리 정의된 구간과 그 평균을 사용하지만, Isotonic Regression은 구간 경계와 예측값을 함께 최적화 함.

• 목표

  • 입력된 예측값 $\hat{p}_i$를 사용하여 정규화된 확률 $\hat{q}_i = f(\hat{p}_i)$를 얻음. \(\min_{\substack{\theta_1,...,\theta_M \\ a_1,...,a_{M+1}}} \sum^M_{m=1}\sum^n_{i=1} 1 (a_m \leq \hat{p_i} < a_{m+1})(\theta_m - y_i)^2,\) \(\text{subject to $0 = a_1 \le a_2 \le ... \le a_{M+1} = 1, \quad \theta_1 \le \theta_2 \le ... \le \theta_M.$}\)

Platt Scaling ¹⁰

• Parametric 방식으로 로지스틱 회귀를 통해 예측 확률을 Calibration함.

• 분류기의 비 확률적 예측값을 로지스틱 회귀 모델의 입력으로 사용하며, 두 개의 스칼라 파라미터 $a$와 $b$를 학습함.

  • 이러한 파라미터들은 비확률적 출력 $z$를 확률값으로 변환하는 데 사용되며, NLL 손실에 의해 검증 데이터셋에서 최적화됨.
  • Platt scaling이 적용되는 동안 신경망의 다른 파라미터들은 고정되어 변경되지 않음. \(\hat{q}_i = \sigma(az_i + b).\)

     

다중 분류에 Calibration 적용하기

• Guo, Chuan et al. 은 Temperature scaling을 통해 Calibration을 후처리로 수행하는 방식을 제안함. ¹

Binning Method를 다중 클래스로 확장하기

• Binary Calibration으로 전환

  • 각 클래스 $k$에 대하여 one-vs-all 문제를 형성함
    • $y_i = k$인 경우 1, 아닌 경우 0
    • 예측 확률
      \(\sigma_{\text{SM}}(z_i)^{(k)}.\)

• Calibration 적용

  • 각 클래스에 대해 Binary calibration 모델 $K$개 생성
  • 테스트 시, $[\hat{q}_i^{(1)}, …, \hat{q}_i^{(K)}]$ 의 비정규화 확률 벡터 획득

    • 새로운 클래스 예측
      \(\hat{y}_i ' = \text{argmax}_k \,\,\hat{q}_i ^{(k)}.\)

    • 새로운 Confidence 예측
      \(\hat{q}_i ' = \max_k \hat{q}_i^{(k)} / \sum_{k=1}^K \hat{q}_i^{(k)}.\)

  • Histogram binning, Isotonic regression 등에 적용 가능

Platt Scaling을 다중 클래스로 확장하기

• Matrix Scaling

  • 로그 벡터 $z_i$에 선형 변환 $W z_i + b$ 적용
    \(\hat{q}_i = \max_k \sigma _{\text{SM}} (W z_i + b) ^{(k)}.\)

  • 새로운 클래스 예측
    \(\hat{y}_i ' = \text{argmax}_k (W z_i + b)^{(k)}.\)

  • W와 b는 검증 데이터에 대한 NLL 최소화로 최적화함

    • 파라미터 수는 클래스 수 $K$에 따라 증가함.
• Vector Scaling
  • Matrix scaling의 변형이며, $W$를 대각 행렬로 제한

• Temperature Scaling

  • 모든 클래스에 대해 단일 스칼라 파라미터 $T>0$ 을 사용함.
  • 주어진 로그 벡터 $z_i$에 대해 새로운 Confidence 예측 적용
  • T는 검증 데이터에서 NLL을 기준으로 최적화되며 이는 Softmax 함수의 최대값을 변경하지 않으므로 클래스 예측 $\hat{y}_i ‘$ 는 변경되지 않아 모델의 정확도에 아무 영향도 주지 않음.
  • 목표
    • 주어진 제약 조건에서 로그 벡터에 대한 출력 확률 분포의 엔트로피를 최대화 하는 것 \(\hat{q}_i = \max_k \sigma _{\text{SM}} (\frac{z_i}{T})_k,\) \(\text{where $\sigma_{\text{SM}}$ is a softmax function and $k$ is an index of class.}\)
  • T 해석
    • T > 1: Softmax Output을 부드럽게 하여 엔트로피를 증가시킴
    • T -> inf: Confidence $\hat{q}_i$가 1/K 에 가까워지며 최대 불확실성을 의미함
    • T = 1: 원래의 Confidence $\hat{q}_i$를 복원함
    • T -> 0: Confidence $\hat{q}_i$가 하나의 점 (확률 질량)으로 축소됨 ($\hat{q}_i$ = 1).
  • 구현 예시

import numpy as np
from scipy.optimize import minimize
from tensorflow.keras.losses import sparse_categorical_crossentropy
from tensorflow.keras.activations import softmax

# model은 Softmax를 계산하기 이전 Output까지만 생성해야함.
logits = model.predict(X_val)

# 기본 Softmax 계산
def softmax_fn(logits, temperature=1.0):
    scaled_logits = logits / temperature
    return softmax(scaled_logits, axis=1)

# Temperature 조정 후 NLL(negative log likelihood)을 계산하는 함수
def temperature_scaling_loss(temperature):
    temperature = np.maximum(temperature, 1e-3)  # Zero dividing 문제 방지
    probs = softmax_fn(logits, temperature)
    
    # y_val: 정답 카테고리 (0,1,2,3)
    loss = sparse_categorical_crossentropy(y_val, probs)
    return np.mean(loss)

# T 최적화
result = minimize(temperature_scaling_loss, x0=1.0, bounds=[(0.01, 100.0)])
optimal_temperature = result.x[0]

# 최적의 T를 사용하여 Calibrated 확률 계산
calibrated_probs = softmax_fn(logits, optimal_temperature)

# Calibrated 확률과 기본 확률 비교
original_probs = softmax_fn(logits)
print("Original probabilities:\n", original_probs[:5])
print("Calibrated probabilities:\n", calibrated_probs[:5])

# 예시 Output: 4-Class 분류 문제
Original probabilities:
[[9.99686837e-01 4.67872553e-07 3.06890026e-04 5.80308551e-06]
 [9.99612272e-01 5.80648384e-06 3.51151451e-04 3.07460177e-05]
 [9.97133374e-01 3.59399237e-05 2.61593983e-03 2.14804168e-04]
 [9.95973289e-01 4.75247180e-05 3.75530589e-03 2.23892945e-04]
 [9.99999762e-01 2.49505733e-12 2.24622028e-07 8.51538617e-10]]
Calibrated probabilities:
[[0.6816287  0.05747936 0.17277414 0.08811776]
 [0.6409527  0.08286864 0.16622284 0.10995582]
 [0.5618934  0.09902193 0.20496799 0.1341167 ]
 [0.5515181  0.10193248 0.21395408 0.13259539]
 [0.89758205 0.00964449 0.06682549 0.0259479 ]]

     

---

2. 불확실성 측정의 어려움 ^{2 11 12}

• 불확실성은 일반적으로 하나의 개념이지만 모델링 목적하에 두 가지로 구분할 수 있음.

  • Aleatoric uncertainty ㅣ 데이터 자체의 본질적 불확실성, 입력 공간에서 클래스가 겹치는 것이 원인
    • Softmax 출력은 서로 겹치는 클래스에 대해 중간 확률을 출력 가능 (0~1사이의 확률 출력)
  • Epistemic uncertainty ㅣ 모델이나 파라미터에 대한 불확실성, 학습 데이터 분포에서 벗어난 (Out-of-distribution, OOD) 입력이 원인
    • 학습 데이터와는 완전히 다른 분포 밖의 데이터 OOD에 대해서도 Softmax 출력이 높은 값을 가질 수 있음.
    • Softmax가 낮은 차원의 입력 공간에서 OOD 를 의미 없는 높은 신뢰도로 잘못 예측하기 쉬움.
      • Feature extraction을 할 기회가 적어 최종 층의 특징들이 단순한 변환일 뿐이기 때문.
      • 저차원에서는 OOD 입력이 학습된 데이터의 확대 버전으로 쉽게 생성될 수 있음.
      • Relu는 Homogenous 함수로, 확대된 입력이 확대된 최종 레이어 특성을 생성하여 Softmax 신뢰도를 증가시킴.
    • 고차원에서는 OOD에 대해 더 높은 불확실성을 나타내며 암시적 편향 (Implicit bias) 을 발생시킴.
• Softmax saturation
  • Softmax 출력 값이 너무 높아서 OOD 데이터와 학습 데이터에 대한 신뢰도가 비슷해지는 현상.
• Softmax extrapolation
  • OOD 데이터가 학습 분포보다 높은 신뢰도를 보이는 Softmax 영역으로 매핑될 수 있음.

     

Softmax와 OOD 영역 ²

• Softmax 신뢰도를 통한 불확실성 지표

  • Max predicted probability for any class
  \[U_{\text{max}} = - \max_i \sigma(\mathbf{z})_i.\]
  • Entropy
  \[U_{\text{entropy}} (\mathbf{z}) = - \sum_{i=1}^K \sigma(z)_i \log \sigma (\mathbf{z})_i.\]

• 유효한 OOD 영역 (Valid OOD region)

  • 학습 분포 (Training distribution) ㅣ $x \sim D_{in}$는 학습된 데이터 분포를 나타냄

  • OOD 분포 (또는 Outlier) ㅣ $x \sim D_{out}$은 학습 분포 밖의 데이터를 의미하며, 모델이 접하지 않은 데이터 분포임.

  • $U(z’)$을 z’에 대한 $U_{\text{max}}, U_{\text{entropy}}$ 와 같은 불확실성 지표 (Uncertainty estimator) 라고 했을 때, 유효한 OOD 영역 $R$은 다음과 같이 정의될 수 있음.
  \[R: \{ z' \in \mathbb{R}^H | \mathbb{E}_{z \sim D_{in}} [\mathbb{I}(U(z')>U(z))] > 1 - \epsilon \}\]
  • 해당 정의는 점 $z’$가 $(1-\epsilon) \%$의 학습 데이터보다 불확실해야 하는 영역을 나타냄.
  • $U_{\text{max}}, U_{\text{entropy}}$의 경우, 학습 분포의 95% 보다 Decision boundary 에 가까워 져야 OOD 데이터가 유효한 OOD 영역에 포함됨.
    • 이는 OOD 데이터가 Decision boundary 가까이 있도록 불확실성을 많이 가져야한다는 의미임.

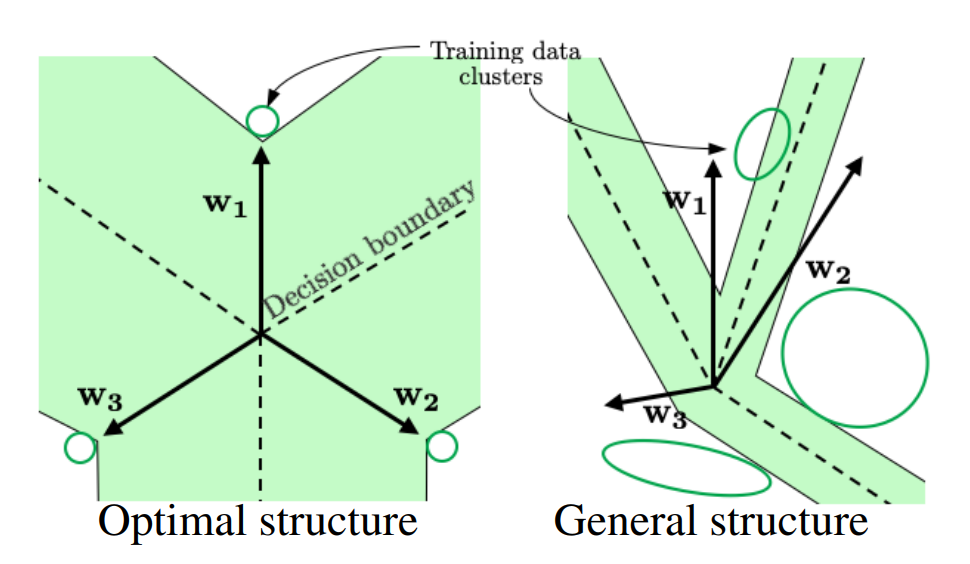The valid OOD region.²

• Decision boundary 구조를 통해 OOD 데이터를 감지하는 것은 유의미하지만, 독립적으로 사용하기엔 충분하지 않음.

     

Softmax 신뢰도와 불확실성 정량화 ²

• CNN에서 학습된 필터들은 특성 패치를 감지하며, 이 패치들이 필터와 일치하면 최대로 활성화 됨.
  • OOD 데이터는 이러한 구별 특징이 없기 때문에 낮은 크기의 활성화를 발생시키고, 최종적으로 OOD 입력은 비정상적인 최종 층 활성화 패턴을 생성하게 됨.

• 최종 층 활성화 크기
  \(||z||\)

• 활성화 친숙도 (Activation familarity)
  \(\max_i \cos \theta_{i, z},\) \(\text{where $\theta_{i,z}$ is the angle between $w_i$ and $z$.}\)

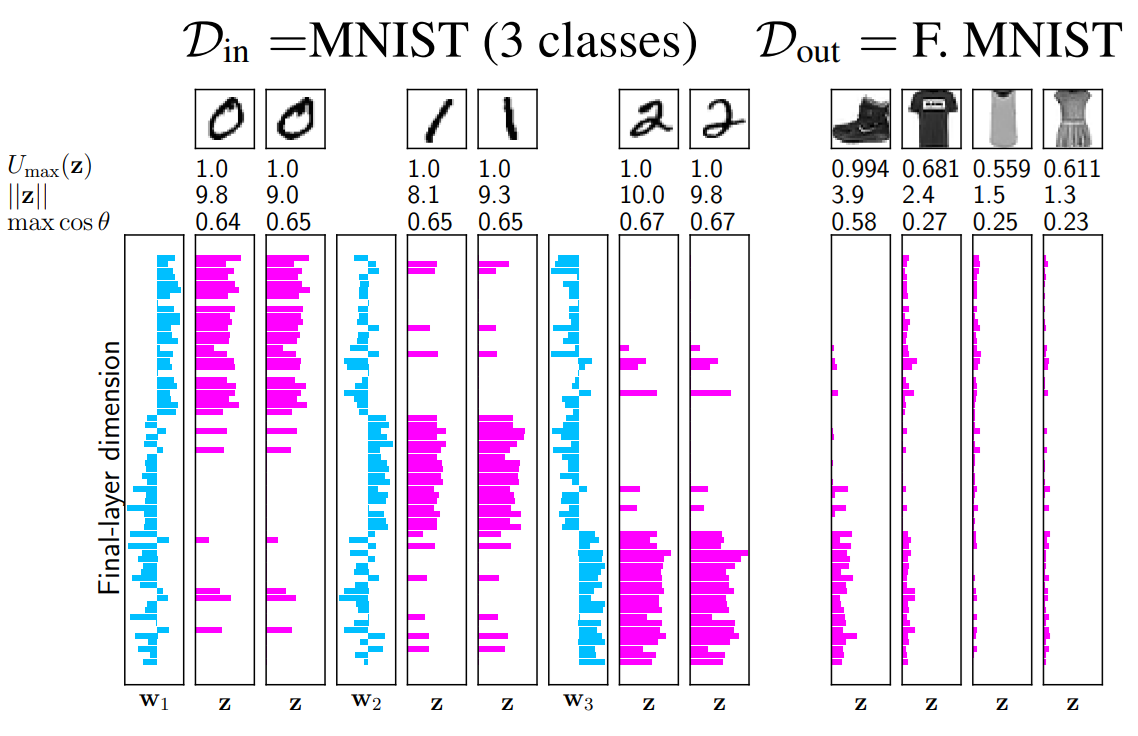Activation patterns of the last layer form trained Lenet. OOD show the abnormal patterns. ²

     

• Softmax 신뢰도에 미치는 영향

  • Softmax 함수를 다음과 같이 표현 가능함
    \(\sigma(z)_i = \frac{\exp (||w_i|| \cdot ||z|| \cdot \cos \theta_{i,z})}{\sum_j \exp (||w_j|| \cdot ||z|| \cdot \cos \theta_{j,z})}.\) \(\text{The absolute value of} \,\, z \,\, \text{plays the same role as the temperature parameter in Platt scaling.}\)

  • Softmax 신뢰도에 대해 $z$ 와 $\cos \theta_{i, z}$가 주는 효과를 분석 가능함.
  • 최적의 Decision boundary 구조와 결합될 때, 낮은 친숙도는 신뢰도를 감소시킴.

• Mental model

  • 고차원에서 Softmax 신뢰도의 동작을 이해하기 위한 모델
  • 전제 조건
    • 네트워크의 Decision boundary 구조가 최적화되어 있다고 가정.
    • 대부분의 각도에 대하여, $\cos \theta_{i,z} = - \frac{1}{K-1}$ 라고 가정.
  • 이 모델은 학습 데이터의 특징의 강도와 친숙도가 모두 감소할 때 불확실성이 증가함을 설명함 \(U_{\text{max mental}} (z) = - \frac{1}{1 + (K-1) \exp (- ||z|| (\frac{1}{K-1} + \max \cos \theta_{i,z}))},\) \(\text{where $\max \cos \theta_{i, z} \in [-1, 1]$ represents the familarity of the combination}\) \(\text{of final-layer features relative to the training data}.\)

     

Conclusion

• 딥러닝 모델의 확신 및 신뢰도 문제는 기술적, 윤리적 관점에서 중요한 이슈로 여겨질 수 있으며, 이러한 문제에 대한 Calibration 방법론 개발은 필수적이라 여겨짐.
• 안전하고 신뢰가능한 인공지능 모델 개발을 위해, Calibration을 효과적으로 적용하여 딥러닝 모델의 신뢰성을 높이는 작업이 필요함.

     

References

1. Guo, Chuan, et al. “On calibration of modern neural networks.” Inter ↩ ↩² ↩³ ↩⁴ ↩⁵

2. Pearce, Tim, Alexandra Brintrup, and Jun Zhu. “Understanding softmax confidence and uncertainty.” arXiv preprint arXiv:2106.04972 (2021). ↩ ↩² ↩³ ↩⁴ ↩⁵ ↩⁶

3. Why is softmax output not a good uncertainty measure for Deep Learning models? ↩

4. Quantifying Uncertainty in Neural Networks ↩

5. Szegedy, Christian, et al. “Intriguing properties of neural networks.” arXiv preprint arXiv:1312.6199 (2013). ↩

6. Softmax Activation Function Explained ↩

7. Naeini, Mahdi Pakdaman, Gregory Cooper, and Milos Hauskrecht. “Obtaining well calibrated probabilities using bayesian binning.” Proceedings of the AAAI conference on artificial intelligence. Vol. 29. No. 1. 2015. ↩

8. Zadrozny, Bianca, and Charles Elkan. “Obtaining calibrated probability estimates from decision trees and naive bayesian classifiers.” Icml. Vol. 1. 2001. ↩

9. Zadrozny, Bianca, and Charles Elkan. “Transforming classifier scores into accurate multiclass probability estimates.” Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. 2002. ↩

10. Platt, John. “Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods.” Advances in large margin classifiers 10.3 (1999): 61-74. ↩

11. Gal, Yarin, and Zoubin Ghahramani. “Dropout as a bayesian approximation: Representing model uncertainty in deep learning.” international conference on machine learning. PMLR, 2016. ↩

12. Nguyen, Anh, Jason Yosinski, and Jeff Clune. “Deep neural networks are easily fooled: High confidence predictions for unrecognizable images.” Proceedings of the IEEE conference on computer vision and pattern recognition. 2015. ↩