VAE 제대로 알기 | Variational Auto Encoder

🪗 Variational Auto Encoder(VAE)를 살펴보고, 그 수식과 이론을 이해해봅시다.

Posted Mar 19, 2025

By Seoyoung Oh

38 min read

KEYWORDS
VAE, Variational Auto Encoder, VAE 설명, VAE Paper, VAE Loss, VAE Architecture, VAE GAN

Original Paper Review | Tutorial on Variational Autoencoders

Introduction

최근 몇 년 사이, 인공지능 분야에서 생성 모델(Generative Model)에 대한 관심이 증가하고 있습니다.
- 생성 모델은 단순히 데이터를 분류/예측할 뿐만 아니라, 새로운 데이터를 직접 생성하는 능력을 갖춘 모델을 의미합니다.
- 모델이 주어진 데이터의 분포 $P(X)$를 학습한 뒤, 그와 유사한 새로운 예제를 만들어내는 것을 목적으로 합니다.
  - 여기서 $X$는 이미지와 같은 데이터 포인트를 나타내며 보통 수천 개의 픽셀로 구성되어 있기 때문에, 각 픽셀은 하나의 값이 아니라 다른 픽셀들과의 복잡한 관계를 맺고 있습니다.
  - (ex. 인접한 픽셀은 비슷한 색을 띠거나 동일한 물체의 일부일 가능성이 높음)
- 좋은 생성 모델은 단순히 데이터의 개별 요소만 파악하는 것이 아니라, 데이터 내부의 구조적 상관관계까지 학습해야 합니다.
수학적으로 데이터 분포 $P(X)$를 정의하거나 계산하는 것은 가능하지만, 이것만으로는 충분하지 않습니다.
- 어떤 이미지가 실제 데이터로부터 얼마나 멀리 떨어져 있는지는 판단할 수는 있지만, 그것이 곧 새롭고 의미 있는 데이터를 생성할 수 있다는 뜻은 아닙니다.
- 진정한 생성 모델의 가치는, 기존 데이터셋과 유사하면서도 새로운 예제들을 창의적으로 생성해낼 수 있는 능력에 있습니다.
이러한 생성 모델의 한계를 극복하고 실용적인 접근을 제시한 방법 중 하나가 바로 Variational Autoencoder(VAE)입니다.
- VAE는 데이터의 분포를 확률적으로 근사하고, 이를 바탕으로 새로운 데이터를 샘플링할 수 있는 모델입니다.
- 아래의 전통적인 생성 모델들의 단점을 VAE는 상당 부분 해결합니다.
  - 강한 전제조건 ㅣ 데이터 구조에 대해 지나치게 엄격한 가정을 필요로 함
  - 과도한 근사 ㅣ 복잡한 분포를 지나치게 단순화하여 본질을 놓침
  - 계산 자원의 한계 ㅣ MCMC(Markov Chain Monte Carlo) 같은 방식은 현실적으로 매우 느림
- VAE는 신경망을 이용하여 데이터 분포를 유연하게 학습하며, 비교적 간단한 근사와 빠른 역전파(Back-propagation)만으로도 학습이 가능합니다.

잠재 변수 모델 ^{Latent Variable Models}

잠재 변수 $z$는 우리가 관측할 수 없지만, 데이터 생성에 결정적인 영향을 미치는 숨겨진 요인을 의미합니다.
- 눈에 보이지 않지만 실제 이미지를 만들어내는데 중요한 역할을 하는 내재된 정보라고 할 수 있습니다.
- ex. 0부터 9까지의 숫자 손글씨 이미지를 생성한다고 가정했을 때, 모델이 숫자 이미지를 생성하려면 먼저 어떤 숫자를 만들 것인지를 결정해야 합니다.
  - 숫자 $5$를 만들지 $0$을 만들지는 잠재 변수 $z$에 의해 결정되며, 이 결정에 따라 생성되는 이미지의 특징도 자연스럽게 달라지게 됩니다.
- 즉, 잠재 변수는 생성 과정에서 중간 단계의 역할을 하며, 생성된 이미지의 일관성과 정합성이 보장되게 합니다.
문제는 우리가 어떤 이미지 $X$를 봤을 때, 그것을 만들어낸 정확한 잠재 변수 $z$의 값을 직접 알 수 없다는 점입니다.
- 따라서 잠재 변수를 추정(Infer)하는 방법이 필요하며, 이는 컴퓨터 비전 및 딥러닝에서 중요한 연구 주제가 되어왔습니다.
좋은 생성 모델의 조건
- VAE와 같은 생성 모델은, 잠재 변수 $z$를 잘 설정했을 때 신뢰할 수 있는 이미지 $X$를 생성할 수 있어야 합니다.
- $z$가 의미 있는 정보를 담고 있어야 하며, 데이터셋의 전체 분포를 잘 반영하도록 구성되어야 합니다. $P(X) = \int P(X|z; \theta) P(z) dz$
  - $P(X)$ ㅣ 관측 데이터 $X$의 전체 분포
  - $P(z)$ ㅣ 잠재 변수의 분포(보통 정규분포로 가정함.)
  - $P(X \vert z; \theta)$ ㅣ 주어진 $z$에 따라 $X$가 생성될 확률
- 모델의 목적는 위 수식에서 우변의 적분을 최대화하는 것
  - i.e., 주어진 분포 $P(z)$로부터 유의미한 $X$를 최대한 잘 생성할 수 있도록 학습하는 것입니다.
VAE와 가우시안 출력
- VAE에서는 생성 모델 $P(X|z; \theta)$를 다음과 같은 정규분포(Gaussian Distribution)로 가정합니다: $P(X|z; \theta) = N(X|f(z; \theta), \sigma^2 I)$
  - $f(z; \theta)$ ㅣ 잠재 변수 $z$를 입력으로 하여 이미지의 평균값을 출력하는 신경망
  - $\sigma^2 I$ ㅣ 공분산 행렬(Covariance Matrix)로, 생성된 샘플이 항상 같은 값을 갖는 것이 아니라 일정한 노이즈(변화)를 허용하도록 함.
- 이러한 정규분포를 사용하는 이유는 다음과 같습니다:
  - 다양한 출력을 가능하게 함 ㅣ 동일한 $z$에서 생성되는 $X$는 항상 동일하지 않으며, 유사하지만 서로 다른 다양한 샘플들을 만들 수 있습니다.
  - 학습에 유리함 ㅣ 정규분포는 미분 가능하고, 경사하강법과 같은 최적화 기법을 적용하기에 이상적입니다.
  - 데이터의 연속적 특성을 반영 ㅣ 이미지는 대체로 연속적인 특성을 가지므로, 정규분포는 이를 자연스럽게 표현할 수 있습니다.
Dirac Delta 함수와 VAE
- Dirac Delta 함수는 수학적으로는 함수처럼 보이지만, 실제로는 분포(Distribution) 또는 일반화 함수(Generalized Function)의 일종입니다.
  - $\delta(x)$는 $x=0$에서만 무한대의 값을 가지고, 나머지 구간에서는 $0$이며, 전체 적분은 1이 되는 성질을 가집니다:
    $\int _{-\infty} ^{\infty} \delta (x) dx = 1, \quad \delta (x \neq 0) = 0.$
  - 이 함수는 실제 확률 분포가 아닌, 무한히 정확한 지점만을 갖는 매우 이상적인 경우를 가정합니다.
- Dirac Delta Function을 사용하지 않는 이유
  - VAE에서 사용하는 사후 분포 $Q(z \vert X)$는 연속적인 확률 밀도 함수(보통 Gaussian)으로 가정되는데,
    - 만약 $Q(z \vert X)$가 Dirac Delta 함수였다면, 이는 잠재 변수 $z$가 단 하나의 지점에서만 정의된다는 뜻이며, 이는 샘플링이 아닌 단순한 함수 출력이 되어버립니다.
    - i.e., 오토인코더의 인코더처럼 작동하게 되며, 각 $z$는 오직 하나의 $X$만 생성할 수 있게 됩니다.
  - 하지만 VAE는 “확률적 오토인코더”이기 때문에, 사후 분포 $Q(z \vert X)$에서 샘플링할 수 있어야 하며, 이때 Reparameterization Trick을 통해 미분 가능한 방식으로 샘플링이 가능해야 합니다.
    - Dirac Delta 함수는 이를 불가능하게 만듭니다:
      - Dirac Delta 함수는 미분이 불가능하여 Back-propagation에 사용할 수 없습니다.
      - 확률 분포로서의 성질이 약하며, 샘플링 가능성이 없습니다.
      - 잠재 변수 공간을 탐색할 수 없게 되어 잠재 공간의 의미 있는 구조 학습이 어렵습니다.
  - 따라서 VAE에서는 $Q(z \vert X)$를 $\mu(X)$과 $\sigma^2(X)$을 가지는 정규분포 $\mathcal{N}(\mu(X), \sigma^2(X))$로 가정하며, 이것들은 학습 가능한 파라미터로 설정됩니다.
VAE 모델의 구조
- 고정된 모델 파라미터 $\theta$ 하에서 $z$와 $X$를 반복적으로 샘플링할 수 있음을 의미합니다.

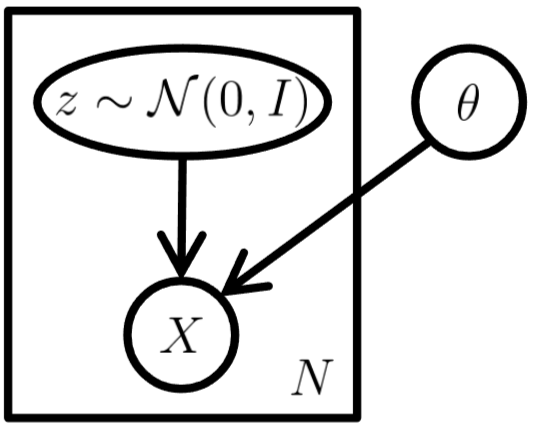The standard VAE model represented as a graphical model ¹.

Variational Auto-encoder(VAE)

VAE는 잠재 변수(Latent Variable) $z$에서 데이터 $X$로의 복잡한 Mapping을 신경망을 통해 학습하는 방식입니다.
전통적인 오토인코더(Auto-encoder, AE)는 입력 데이터를 압축하여 잠재 공간에 Mapping하고, 다시 그 잠재 공간에서 원래 데이터를 복원하는 방식이지만,
- VAE는 잠재 공간의 분포를 모델링하고, 이를 바탕으로 새로운 데이터를 생성하는 데 초점을 맞춥니다.
샘플링 및 가능도 추정(Likelihood Estimation)
- VAE는 데이터의 가능도 $(P(X))$를 샘플링을 통해 근사합니다.
- 이를 위해 잠재 공간에서 샘플링을 진행하고, 이 샘플을 이용해 데이터가 생성될 확률을 계산합니다 (단순 분포로부터 데이터의 가능도를 추정하는 것).
- 이 과정에서 MCMC(Markov Chain Monte Carlo)와 같은 계산적으로 비효율적인 방법을 사용하지 않고, 확률적 경사 하강법(Stochastic Gradient Descent, SGD)을 사용하여 가능도를 최대화하는 방향으로 학습합니다.
- 이 방법은 빠르고 실용적인 학습을 가능하게 하며, 복잡한 샘플링 방법을 피할 수 있습니다.

가정과 목적 함수 ^{Objective Function}

VAE에서 샘플링의 목적
- 입력 데이터 $X$의 가능도 $(P(X))$를 잠재 변수 $z$를 기반으로 계산하는 것입니다.
- 이때 잠재 변수 $z$는 데이터 $X$를 생성할 가능성이 높은 변수들이며, 모델이 학습할 때 이러한 변수들을 효과적으로 샘플링하여 $X$와 유사한 새로운 데이터를 생성하는 것을 목표로 합니다.
함수 $Q(z \vert X)$는 데이터 $X$에 대해 의미 있는 $z$ 값에 집중할 수 있게 하여 샘플링 과정을 효율적으로 만듭니다.
- 모델은 모든 가능한 잠재 변수 $z$를 고려하는 대신, $X$를 생성할 가능성이 높은 잠재 변수들만을 샘플링함으로써 학습의 효율성을 높일 수 있습니다.
Kullback-Leibler Divergence(KL Divergence)
- KL 발산(KL Divergence)은 하나의 확률 분포가 다른 확률 분포에서 얼마나 벗어나는지를 측정하는 지표입니다.
- VAE에서는 KL 발산을 사용하여 $Q(z)$와 실제 사후 분포 $P(z \vert X)$ 간의 차이를 측정합니다.
- 이 차이를 최소화하는 것이 VAE의 주요 목표 중 하나이며, KL 발산은 다음과 같이 표현됩니다: $D[Q(z) \vert P(z|X)] = E_{z \sim Q} [\log Q(z) - \log P(z \vert X)].$
  - 위 식은 $Q(z)$와 실제 사후 분포 $P(z \vert X)$ 간의 차이를 정량화합니다.
  - KL 발산을 최소화하려는 과정은 $Q(z)$가 실제 사후 분포 $P(z \vert X)$에 근접하게 되도록 최적화하는 과정입니다.
기대값(Expectation) 간의 관계
- 다음은 베이즈 정리(Bayes’ Rule)를 이용하여 $P(X)$와 $P(X \vert z)$ 간의 관계를 보여주는 식입니다: $D[Q(z) \| P(z|X)] = E_{z \sim Q} [\log Q(z) - \log P(X|z) - \log P(z)] + \log P(X)$
  - $Q(z)$가 $P(z \vert X)$와 얼마나 일치하는지, $P(X)$를 최대로 만들기 위한 조건들을 보여줍니다.
  - 위 관계를 바탕으로, VAE는 $Q(z \vert X)$를 통해 $P(z \vert X)$를 근사하고, 이를 통해 데이터 $X$를 효율적으로 생성할 수 있습니다.
로그 확률((Log Probability)) 최대화
- 위 식에서 목적은 $\log P(X)$를 최대화하는 것입니다.
- 이를 위해 $Q(z \vert X)$와 $P(z \vert X)$ 간의 KL 발산을 최소화해야 합니다: $\log P(X) - D[Q(z \vert X) \vert P(z \vert X)] = E_{z \sim Q} [\log P(X \vert z)] - D[Q(z \vert X) \vert P(z)]$
  - $Q(z \vert X)$가 $P(z \vert X)$에 가깝게 구성되도록 최적화되는 과정을 나타냅니다.
  - 이 과정을 통해, 모델은 데이터 $X$의 가능도를 최적화하고, 새로운 데이터를 생성할 수 있게 됩니다.
수렴과 최적화(Convergence and Optimization)
- 만약 $Q(z \vert X)$가 $P(z \vert X)$를 정확하게 근사할 수 있다면, KL 발산은 0이 되고 $\log P(X)$를 직접 최적화할 수 있습니다.
- 이는 Variational Inference 방법을 도입하여, 복잡한 사후 분포 $P(z \vert X)$를 더 간단한 분포인 $Q(z \vert X)$로 모델링할 수 있게 합니다.

목적 함수 최적화 ^{Objective Function}

VAE는 Feed-forward 신경망으로 구현되며, $P(X \vert z)$는 가우시안 분포로 모델링됩니다.
(Left) Reparameterization Trick 없이 구현된 모델 ㅣ (Right) Reparameterization Trick으로 구현된 모델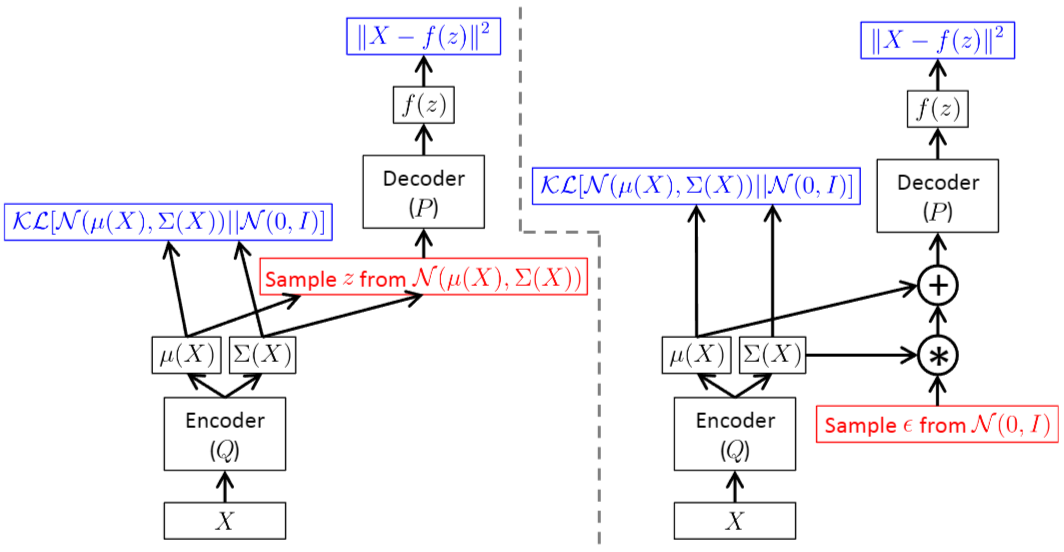 A training-time VAE implemented as a feed-forward neural network, where $P(X \vert z)$ is Gaussian ¹.
- 빨간색은 미분 불가능한 샘플링 연산을 나타내며, 파란색은 손실 함수를 나타냅니다.
- 두 신경망은 Feed-forward 동작이 동일하지만, 오른쪽 네트워크에서는 역전파를 적용할 수 있습니다.
학습 목적 ㅣ 가능도 극대화와 KL 발산 최소화
- 목표는 데이터의 가능도 $P(X)$를 최대화하면서, 두 확률 분포인 근사 사후 분포 $Q(z \vert X)$와 사전 분포 $P(z)$ 간의 KL 발산을 최소화하는 것입니다.
$Q(z \vert X)$ 모델링
- $Q(z|X)$는 보통 다변량 가우시안 분포(Multivariate Gaussian Distribution)로 모델링됩니다: $Q(z|X) = N(z|\mu(X; \theta), \Sigma(X; \theta))$
- 여기서 $\mu$와 $\Sigma$는 데이터로부터 학습되는 결정적 함수이며, $\theta$는 모델 파라미터입니다.
KL 발산 계산
- 두 다변량 가우시안 간의 KL 발산은 다음과 같이 계산됩니다: $D[Q(z) \| P(z)] = \frac{1}{2} \left( \text{tr}(\Sigma_1^{-1} \Sigma_0) + (\mu_1 - \mu_0)^{\top} \Sigma_1^{-1} (\mu_1 - \mu_0) - k + \log\left(\frac{\det \Sigma_1}{\det \Sigma_0}\right) \right)$
- $k$는 분포의 차원수이며, 이 항은 KL 발산의 효율적인 평가와 최적화에 도움을 줍니다.
그래디언트(Gradient) 계산과 Reparameterization Trick
- $E_{z \sim Q}[\log P(X \vert z)]$의 기대값을 추정하기 위해, $Q(z \vert X)$로부터 샘플 $z$를 추출합니다.
- 이 과정에서 $\log P(X \vert z)$는 $P$와 $Q$에 의존하기 때문에, 샘플링이 역전파 과정에서 그래디언트 흐름을 방해하지 않도록 주의해야 합니다.
- Reparameterization Trick을 사용하여, $z$를 다음과 같이 표현합니다:
  $z = \mu(X) + \Sigma^{1/2}(X) \cdot e, \quad \text{where} \quad e \sim N(0, I).$
  - 여기서 $e \sim N(0, I)$는 표준 정규 분포에서 샘플링된 벡터입니다.
- $z$가 $X$의 결정적 함수로 표현되어 그래디언트 계산이 가능해지며, 학습 효율성을 높일 수 있습니다.
최적화하려는 최종 방정식은 다음과 같습니다:
$E_{X \sim D} \left[ E_{z \sim Q} \left[ \log P(X|z) \right] - D[Q(z|X) \| P(z)] \right]$
- 가능도 최대화와 KL 발산 최소화라는 두 가지 목표를 동시에 달성하는 최적화 문제를 나타냅니다.
- 이 식을 SDE을 사용하여 최적화할 수 있습니다.

추론(테스트)

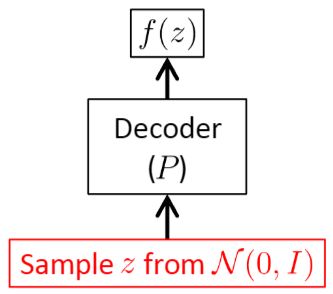The testing-time VAE ¹

VAE 모델 추론은 새로운 샘플을 생성하는 과정을 뜻하며, 인코더는 제외되고 디코더만 사용됩니다.
새로운 샘플은 표준 정규 분포에서 샘플링된 값 $z \sim N(0, I)$을 디코더로 입력하여 생성됩니다.
확률 평가
- 생성된 샘플들의 확률 $P(X)$는 일반적으로 직접 계산하기 어렵습니다.
- $D[Q(z \vert X) \vert P(z \vert X)]$는 KL 발산을 나타내며, 이 값은 양수입니다.
- 이는 $P(X)$에 대한 Lower Bound으로 작용합니다.
  - 이 Lower Bound은 VAE 모델이 학습 데이터를 얼마나 잘 표현하는지에 대한 통찰을 제공하며, 학습된 모델 하에서 생성된 샘플들이 얼마나 가능성 $(P(X))$이 높은지를 나타냅니다.
$P(X)$를 근사하기 위해, $Q(z)$에서 샘플링하는 것이 유용합니다.
- 이 방법은 $N(0, I)$와 같은 사전 분포에서 샘플링하는 것보다 수렴 속도가 빠릅니다.

목적 함수 해석하기

VAE는 데이터의 가능도인 $\log P(X)$를 최적화하려고 시도하지만, 이를 수행하는 과정에서 근사를 사용합니다.
\[D[Q(z \vert X) \vert P(z \vert X)]\]
- 위 항은 KL 발산으로, 근사 분포인 $Q(z \vert X)$가 실제 사후 분포인 $P(z \vert X)$와 얼마나 잘 일치하는지 측정합니다.
- 이 항을 최적화하는 것은 오차가 생길 수 있는데, 정확한 사후 분포는 복잡하고 계산하기 어려운 경우가 많기 때문입니다.
$\log P(X)$
- 모델 하에서 관측된 데이터의 가능도이며, 이를 최대화하면 재구성된 샘플이 원본 데이터와 유사해지도록 합니다.
VAE의 오류는 아래의 두 항을 균형 있게 조정하는 과정에서 발생합니다.
- $Q(z \vert X)$가 $P(z \vert X)$의 정확한 근사치일 경우, KL 발산 항은 작아지며 모델이 잘 작동합니다.
- 반대로, KL 발산이 커지면 이는 모델 성능이 좋지 않음을 나타내며, 데이터 생성 능력에 영향을 미칠 수 있습니다.
정보 이론(Information Theory)과의 관계
- 최소 설명 길이(MDL, Minimum Description Length)라는 개념을 통해 정보 이론과 연결됩니다.
- 목적 함수의 값이 낮을수록, 모델은 데이터를 더 효율적으로 코드화(Coding of the Data)하는 것에 해당합니다.
- 즉, 모델은 더 적은 비트로 중요한 정보를 더 잘 인식하게 됩니다.
- 이 접근법은 Variational Inference Framework를 통해 얻은 효율성을 이해하는 데 도움을 줍니다.
  - 선택된 근사 분포 $Q(z \vert X)$가 불필요한 오버헤드를 최소화해야 합니다.
$\sigma$ Tuning과 정규화
- $P(X \vert z)$에서 $\sigma$ Tuning은 정규화의 한 형태로 볼 수 있습니다.
- 희소 오토인코더(Sparse Auto-encoder)에서 사용되는 파라미터와 유사하며, 모델의 복잡도를 제어하고 과적합을 방지하는 역할을 합니다.

$D[Q(z \vert X) \vert P(z \vert X)]$에서의 오류

$Q(z \vert X)$와 $P(z \vert X)$
- $Q(z \vert X)$는 입력 $X$에 대한 잠재 변수 $z$의 근사 사후 분포입니다.
- $P(z \vert X)$는 입력 $X$에 대해 잠재 변수 $z$의 실제 사후 분포입니다.
$D[Q(z \vert X) \vert P(z \vert X)]$는 KL 발산으로, 이 항은 두 분포 간의 차이를 측정합니다.
- 이 발산은 근사 분포인 $Q(z \vert X)$를 사용할 때, 실제 분포인 $P(z \vert X)$에 비해 손실되는 정보를 양적으로 나타냅니다.
실제 분포로의 수렴
- 모델의 출력 분포인 $P(X)$가 실제 분포에 수렴하려면, $D[Q(z \vert X) \vert P(z \vert X)]$가 0에 가까워져야 합니다.
- $Q(z \vert X)$가 $P(z \vert X)$를 정확하게 근사해야 한다는 의미입니다.
Zero Divergence 달성의 어려움
- $\mu(X)$과 $\Sigma(X)$을 위해 복잡한 함수를 사용하는 것으로는, $Q(z \vert X)$가 $P(z \vert X)$를 충분히 근사한다고 해서 제로 발산을 보장하는 것은 아닙니다.
- 이 관계를 조절하는 함수 $f$가 이 결과에 큰 영향을 미칠 수 있습니다.
- $P(z \vert X)$가 모든 $X$에 대해 가우시안 분포가 되도록 보장하는 충분히 유연한 함수 $f$가 존재할 수 있습니다.
  - 만약 존재한다면, $\log P(X)$를 최대화하는 것이 가능하며, $D[Q(z \vert X) \vert P(z \vert X)]$의 발산을 최소화하는데 도움이 됩니다.
일반적인 결과 증명의 어려움
- 모든 분포에 대해 일반적인 결과를 증명하는 것은 여전히 해결되지 않은 문제이며, 일부 1D 사례에서는 이론적으로 증명되었습니다.

정보 이론적 해석 ^{Information Theory}

최소 설명 길이 원리(Minimum Description Length Principle)
- 데이터를 인코딩하는 데 필요한 비트 수를 최소화하는 모델이 가장 좋은 모델임을 제시하는 이론입니다.
- VAE에서 $-\log P(X)$는 이상적인 인코딩 전략을 사용하여 데이터 $X$를 인코딩하는 데 필요한 총 비트 수를 나타냅니다.
1단계 ㅣ 잠재 변수 $z$ 인코딩
- 일부 비트는 잠재 변수 $z$를 결정하는 데 사용됩니다.
- KL 발산 $D[Q(z \vert X) \vert P(z)]$는 $P(z)$ (Uninformative)에서 $Q(z \vert X)$ (사후 분포)로 이동하는 데 필요한 추가 정보를 정량화합니다.
- 이는 잠재 변수 $z$에 대한 정보를 관찰된 데이터 $X$로부터 얻을 때 얼마나 많은 정보가 추가되는지를 측정합니다.
2단계 ㅣ 디코딩
- $P(X \vert z)$는 $z$가 결정된 후에 $X$를 재구성하는 데 필요한 정보의 양을 측정합니다.
$X$를 정확하게 표현하는 데 필요한 총 비트 수는 1,2 단계에서 사용된 비트 수의 합이며, KL 발산으로 인한 패널티는 $Q(z \vert X)$가 $P(z)$와 얼마나 잘 일치하는지를 나타냅니다.
- 이 패널티는 인코딩 과정의 비효율성을 반영하며, 최적이 아닌 인코딩이 과도한 비트를 필요로 한다는 점을 보여줍니다.

정규화 파라미터 ^{Regularization Parameter}

전통적인 Sparse AE에서는 정규화 파라미터 $\lambda$가 목적 함수에 사용됩니다. $L = \| \phi( \psi(X) ) - X \|^2 + \lambda \| \psi(X) \|_0$
- $\phi$와 $\psi$는 각각 인코더와 디코더 함수이고, $\| \cdot \|_0$는 희소성을 촉진하는 L0 Norm입니다.
VAE는 전통적인 AE와 달리 별도의 명시적인 정규화 파라미터를 조정할 필요가 없습니다.
Absorption of Constants
- 잠재 변수 $z$의 크기를 조정하여 정규화 파라미터를 도입하는 것(ex. $z' \sim N(0, \lambda I)$)은 모델을 근본적으로 변경하지 않습니다.
- 모델은 동일하게 유지하면서, 상수를 확률론적 정의인 $P$와 $Q$에 흡수시킬 수 있습니다. $f'(z') = f(z'/\lambda), \quad \mu'(X) = \mu(X) \cdot \lambda, \quad \Sigma'(X) = \Sigma(X) \cdot \lambda^2$
출력 분포와 정규화 파라미터
- 연속 데이터를 위한 출력 분포는 일반적으로 가우시안입니다.
  $P(X|z) \sim N(f(z), \sigma^2 I)$
- 로그 확률 $\log P(X|z) = C - \frac{1}{2} \frac{\| X - f(z) \|^2}{\sigma^2}$
  - $C$ ㅣ 상수
  - $\sigma$는 정규화 파라미터처럼 작용하며, 두 항의 균형을 조절합니다.
  - 모델이 데이터를 얼마나 잘 맞추는지 vs 모델이 얼마나 단순해야 하는지
이진(Binary) vs 연속(Continuous) 입력
- 출력 $X$가 이진인 경우, 정규화 파라미터의 행동은 완전히 사라집니다.
  - 오른쪽 두 항이 동일한 정보 단위를 사용하므로 모델이 필요한 정보를 포착하는 데 영향을 미치지 않기 때문입니다.
- 그러나 연속적인 경우에는 $\sigma$를 신중하게 선택해야 하며, 이는 모델의 데이터 $X$ 재구성의 예상 정확도에 영향이 갑니다.

MNIST 데이터와 VAE

MNIST는 손글씨 숫자(0-9) 흑백 이미지 데이터이며, 각 픽셀의 값은 0과 1 사이로 정규화되어 있습니다.
Sigmoid Cross Entropy 손실 함수를 사용하여 잠재 변수 $z$와 주어진 데이터 $X$에 대한 확률 분포 $P(X \vert z)$를 계산합니다.
새로운 데이터 포인트는 다음과 같이 확률적으로 정의됩니다: $X'_i \sim \text{Bernoulli}(X_i)$
- 이는 각 픽셀 값이 Bernoulli Trial로 처리되며, $X_i$는 학습 데이터에서의 실제 관찰 값입니다.
- 이 이진화는 픽셀 표현에서의 불확실성을 인식합니다.
학습 과정
- 모델은 완전히 한 번 학습되며, 손실을 최소화하기 위한 최적의 Learning Rate을 찾기 위해 여러번 수행됩니다.

Samples from a VAE trained on MNIST ¹

VAE의 결과에서, 많은 숫자들이 현실감 있게 생성된걸로 보이지만, 일부 샘플은 숫자들 사이에 위치하는 형태를 보입니다.
- 이는 VAE가 클래스 간 명확한 출력을 생성하기보다는 보간(Interpolation)하는 경향이 있음을 보여줍니다.
- ex. ‘7’과 ‘9’를 섞은 모습
잠재 변수 $z$의 차원 수
- VAE에서 잠재 변수 $z$의 차원 수는 모델 성능에 다양한 영향을 미칩니다.
- 차원이 너무 낮으면(ex. 4 미만) 모델이 데이터의 복잡성을 표현하기 어려워 성능이 나빠집니다.
- 차원이 너무 높으면(ex. 10,000), 모델이 학습 중에 KL 발산 $D[Q(z \vert X) \vert P(z)]$를 낮게 유지하기 어렵습니다.
  - $z$가 클 경우, 근사 분포가 실제 분포와 얼마나 잘 일치하는지를 측정하는 이 차원의 관리가 어려워지기 때문입니다.

Summary

Variational Autoencoder(VAE)는 데이터 생성 모델로, 입력 데이터의 분포를 잠재 변수 $z$를 통해 확률적으로 모델링합니다.
VAE의 학습은 입력 $X$를 재구성하는 손실과 잠재 공간의 정규화(KL Divergence)를 동시에 최소화하는 방식으로 이루어집니다.
정보 이론적으로 보면, 이는 데이터를 압축할 때 필요한 최소 비트 수를 줄이는 방식으로 해석할 수 있습니다.
VAE는 명시적인 정규화 파라미터 없이도 모델 복잡도와 데이터 재현성을 균형 있게 조절할 수 있으며, 잠재 분포는 Dirac Delta가 아닌 연속적인 분포로 설정되어야 샘플링과 학습이 가능합니다.
지나치게 낮거나 높은 잠재 변수의 차원 수는 성능에 부정적인 영향을 줄 수 있으므로 적절한 선택이 중요합니다.

Reference

Doersch, Carl. “Tutorial on variational autoencoders.”, arXiv preprint arXiv:1606.05908 (2016). ↩︎ ↩︎² ↩︎³ ↩︎⁴

인공지능 | AI, AI 이론

This post is licensed under CC BY 4.0 by the author.

VAE 제대로 알기 | Variational Auto Encoder

Introduction

잠재 변수 모델 ^{Latent Variable Models}