ViT 살펴보기 | Vision Transformer

---

KEYWORDS
Vision Transformer (ViT), ViT란, ViT Paper, ViT 모델, ViT 설명, ViT model, ViT 구조, ViT Architecture, ViT 논문리뷰, BEIT, CCT, CVT, DeiT, MobileViT, PvT, Swin Transformer, T2T-VIT

---

     

Original Paper Review | An image is worth 16x16 words: Transformers for image recognition at scale

     

Overview

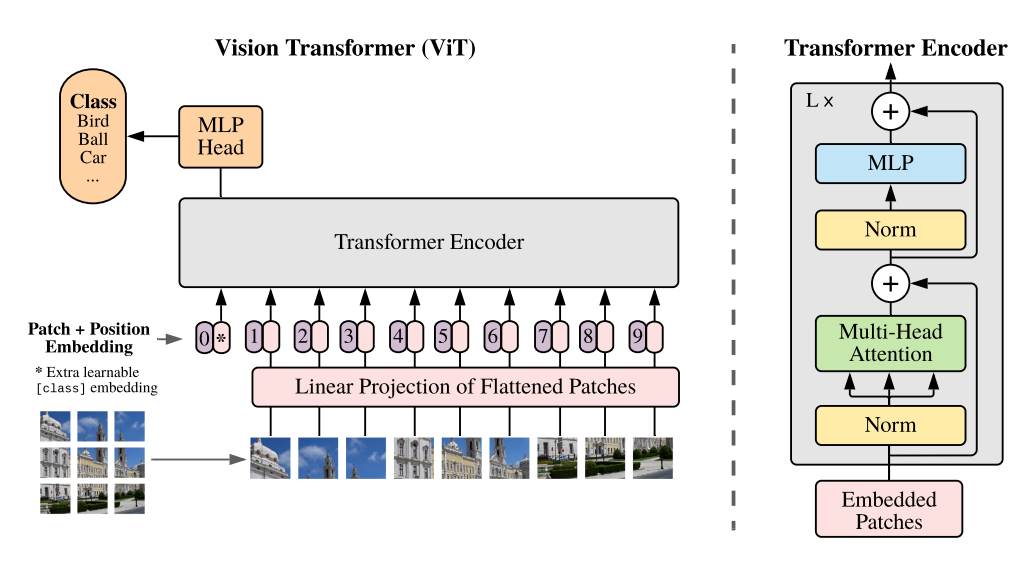
• Vision Transformer(ViT)는 Transformer 구조를 이미지 데이터 처리에 직접 적용한 모델입니다.
  • Image Patch Sequence를 Input으로 하여 기존의 Transformer 구조를 거의 그대로 Vision Task에 활용합니다.
• CNN에 비해 Inductive Bias는 부족합니다.
  ➔ CNN이 가지는 Translation Equivariance 및 Locality 특성을 ViT는 갖추고 있진 않습니다.
  • 이는 ViT가 데이터 전체를 고려하여 Attention할 위치를 정하기 떄문입니다.
• 적은 데이터로 학습할 경우, Resnet50보다 성능이 더 떨어질 수 있습니다.
• Imagenet 21K (1400만 장), JFT-300M (3억 장) 으로 Pre-training, CIFAR-10 (6만 장) 으로 Transfer Learning
• Pretrained model의 크기는 약 300MB

     

Formulation

1. Input

(1) Image

• (C, H, W) = (Channel, Height, Width)

\[x\in\mathbb{R}^{C\times{H}\times{W}}\]

(2) Flatten

• \(P\): 패치 사이즈, \(N\): 이미지 당 패치의 개수

\[x_p \in \mathbb{R}^{N \times (P^2 C)} \quad \text{where} \quad N=\frac{HW}{P^2}\]

(3) Linear Projection

• \(D\): Latent Vector의 크기

\[[x^1_p E; x^2_p E; \cdots ; x^N_p] \in \mathbb{R}^{N \times D} \quad \text{where} \quad E \in \mathbb{R}^{(P^2 C)\times D}\]

(4) Insert the Class Token

• Class token은 BERT의 class token과 유사하며, Embedding patch들 앞에 학습 가능한 token을 추가합니다.
  ➔ Class token \(x_{cls}\) 은 Transformer의 여러 Encoder 층을 거쳐 \(z^0 _L\)로 변환됩니다.
  ➔ 최종적으로 이 값은 이미지에 대한 Representation Vector로 사용됩니다.

\[z_0= [x_{cls}; x^1_p E; x^2_p E; \cdots ; x^N_p] \in \mathbb{R}^{(N+1)\times D}\]

(5) Add the Positional Encoding

Positional Encoding 이란?

\[z_0= [x_{cls}; x^1_p E; x^2_p E; \cdots ; x^N_p] + E_{pos} \in \mathbb{R}^{(N+1)\times D} \quad \text{where} \quad E_{pos} \in \mathbb{R}^{(N+1)\times D}\]

     

2. Transformer Encoder

(1) Multi-Head Self Attention (MSA)

• Query(\(q\)), Key(\(k\)), Value(\(v\)) 간의 관계를 추출합니다.

\[q = z \cdot w_q, \,\, k=z\cdot w_k, \,\, v = z \cdot w_v \quad \text{where} \quad w_q, w_k, w_v \in \mathbb{R}^{D \times D_h}\]

• Self-Attention
  • \(A\): Attention score matrix
  • Attention score가 value(\(v\))와 곱해지면서 query(\(q\))와 key(\(k\))의 연관성이 value(\(v\))에 반영되어 그 중요도를 반영하게 됩니다.
  • \(D^{\frac{1}{2}}_h\) 로 나누는 이유는 Softmax 값이 작은 Gradient를 가지는 것을 방지하기 위함입니다.
  \[SA(z) = A \cdot v \in \mathbb{R}^{N \times D_h} \quad \text{where} \quad A=\text{softmax}(\frac{q \cdot k^T}{\sqrt{D_h}}) \in \mathbb{R}^{N \times N}\]
• Multi-head Self Attention

\[\text{MSA}(z) = [SA_1(z); SA_2(z); \cdots ; SA_k(z)]U_{msa} \quad \text{where} \quad U_{msa} \in (k, D_h, D)\]

(2) Multi-Layer Perceptron (MLP)

• Pre-training ㅣ 1개의 Hidden layer 사용
• Fine-tuning ㅣ 1개의 Linear Layer 사용

(3) Encoder with L layers

• \(L\): Layer 개수

• Layer Normalization ➔ Multi-head Self Attention ➔ Skip Connection

\[z'_l = MSA(LN(z_{l-1})) + z_{l-1},\]

• Layer Normalization ➔ Multi-layer Perceptron ➔ Skip Connection

\[z_l = MLP(LN(z'_l)) + z'_l \quad \text{for} \quad l=1,2,\ldots, L\] \[\text{where} \quad LN(z^j_i) = \gamma \frac{z^j_i - \mu_i}{\sqrt{\sigma^2_i + \epsilon}} + \beta\]

• \(\gamma, \beta\): 학습 가능한 파라미터

3. Output

• Class token \(z^0 _L\) 을 통해 최종 예측이 생성됩니다.
• \(C\): 클래스 개수

\[\hat{y} = LN(z^0_L) \in \mathbb{R}^C \quad \text{where} \quad z^0_L \in \mathbb{R}^D \quad (z_L \in \mathbb{R}^{(N+1) \times D})\]

     

ViT Variants

BEIT (Bidirectional Encoder representation from Image Transformers)

Bao, Hangbo, et al. “Beit: Bert pre-training of image transformers.” arXiv preprint arXiv:2106.08254 (2021).

CCT (Compact Convolutional Transformers)

Hassani, Ali, et al. “Escaping the big data paradigm with compact transformers.” arXiv preprint arXiv:2104.05704 (2021).

CvT (Convolutional vision Transformer)

Wu, Haiping, et al. “Cvt: Introducing convolutions to vision transformers.” Proceedings of the IEEE/CVF international conference on computer vision. 2021.

DeiT (Data-efficient image Transformer)

Touvron, Hugo, et al. “Training data-efficient image transformers & distillation through attention.” International conference on machine learning. PMLR, 2021.

MobileViT

Mehta, Sachin, and Mohammad Rastegari. “Mobilevit: light-weight, general-purpose, and mobile-friendly vision transformer.” arXiv preprint arXiv:2110.02178 (2021).

PvT (Pyramid vision Transformer)

Wang, Wenhai, et al. “Pyramid vision transformer: A versatile backbone for dense prediction without convolutions.” Proceedings of the IEEE/CVF international conference on computer vision. 2021.

Swin Transformer

Liu, Ze, et al. “Swin transformer: Hierarchical vision transformer using shifted windows.” Proceedings of the IEEE/CVF international conference on computer vision. 2021.

T2T-VIT (Tokens-to-Token VIT)

Yuan, Li, et al. “Tokens-to-token vit: Training vision transformers from scratch on imagenet.” Proceedings of the IEEE/CVF international conference on computer vision. 2021.

ViT with Deformable Attention

Xia, Zhuofan, et al. “Vision transformer with deformable attention.” Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2022.

     

---

Reference

1. Dosovitskiy, Alexey. “An image is worth 16x16 words: Transformers for image recognition at scale.” arXiv preprint arXiv:2010.11929 (2020).