음성 신호와 MFCC | Speech Signal and Spectral Features

Posted Oct 31, 2023 Updated Dec 13, 2023

By Seoyoung Oh 15 min read

음성 신호의 개념과 MFCC 기법을 자세히 알아봅시다.

Speech Emotion Recognition (SER)과 같은 task를 위해 머신러닝/딥러닝 모델을 개발하는 경우에, 일반적으로 음성 데이터를 MFCC와 같은 Feature로 변환하여 활용합니다.

이는 음성 내용을 식별하는데 적합한 오디오 구성 요소를 강조하고 배경 소음과 같은 다른 항목들을 삭제하기 위함입니다.

음성 데이터에 대한 Feature Extraction 기법 중 주요 개념을 소개하겠습니다.

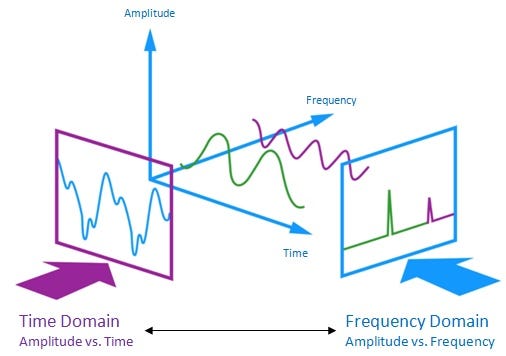
음성 신호란? ^{Audio Signal}

음성 신호는 아래와 같이 시간, 진폭, 주파수 세가지 domain으로 이루어져 있습니다.
- Time (시간) Domain: 음성 신호는 연속적인 샘플 값으로 표현됩니다.
- Amplitude (진폭) Domain: 음성 신호의 강도를 나타냅니다.
- Frequency (주파수) Domain: 음성 신호 주파수의 크기와 분포를 나타냅니다.

음성 데이터는 샘플링 과정을 통해 소리로부터 수집되며 보통 sample rate와 data라는 두가지 요소로 구성됩니다.
Sample rate는 초당 샘플링 횟수를 의미하며, 높은 sample rate 일수록 더 높은 음질의 음성 파일이 저장됩니다.
아래에서 불러온 signal은 158558의 길이를 가지며, sample_rate는 48000Hz 입니다.
- 따라서 (3 x sample_rate)는 3초, 즉 처음 3초 동안의 음성만 인덱싱해서 처리하겠습니다.

  
import scipy.io.wavfile
sample_rate, signal = scipy.io.wavfile.read('test.wav')
signal = signal[0:int(3 * sample_rate)]

음성 분석을 위한 특성 추출 ^{Feature Extraction} | MFCC

사람의 내는 소리 및 음소 (phoneme) 는 혀, 치아 등의 성도 (vocal track) 에 따라 다르게 표현됩니다.
성도의 모양은 Short-time Power Spectrum의 포락선 (envelope) 으로 표현될 수 있으며, MFCC는 이 포락선을 정확하게 포함하기 위해서 생성됩니다.
- 스펙트럼 포락선은 주파수-진폭 평면의 곡선입니다.
MFCC (Mel Frequency Cepstral Coefficents)는 1980년대에 소개되었으며
이 외에도 아래의 특성들을 음성 데이터 분석에 활용할 수 있습니다.
- Zero Cross Rate, Spectral Centroid, Spectral Spread, Spectral Entropy, Spectral Flux, Chroma Vector, Chroma Deviation

Filter Bank

먼저 Filter Bank를 계산한 뒤 몇가지 추가 단계를 거쳐 MFCC를 얻을 수 있습니다.

1. Pre-emphasis Filter를 적용하여 고주파를 증폭하기

$y(t) = x(t) - \alpha x(t-1)$ where $\alpha = 0.95, 0.97$
신호에 Pre-emphasis filter를 적용하여 고주파 대역의 진폭을 증가시키고 낮은 대역의 진폭은 감소시킵니다.
제한된 컴퓨팅 자원으로 개발해야했던 과거에 보편적으로 사용되었습니다. 현대에서는 잘 사용하지 않으며 mean normalization 등으로 대체합니다.
하지만 이 필터는 다음과 같은 장점을 가집니다.
- 보통 고주파는 저주파에 비해 진폭이 작기 때문에 주파수 스펙트럼을 균형있게 유지합니다.
- 푸리에 변환 중 수치적인 문제들을 피하게 해줍니다.
- SNR (Signal-to-Noise Ratio) 를 개선할 수 있습니다.

  
pre_emphasis = 0.97
emphasized_signal = np.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])

2. 신호를 프레임으로 분할 ^Framing

신호는 short-time 프레임으로 분할합니다.
신호 내의 주파수는 시간에 따라 변하기 때문에, 신호 전체에 푸리에 변환을 사용하게 되면 시간에 따른 주파수 형태를 잃게 됩니다.
- 따라서, 신호 내 주파수가 short-time 동안 안정적이라고 가정합니다.
- short-time 프레임에 대해 푸리에 변환을 수행하여 인접한 프레임을 연결합니다.
- 이를 통해 전체 신호의 주파수 형태를 근사할 수 있습니다.
음성 처리에서의 전형적인 프레임 크기는 20ms에서 40ms 입니다.
- 프레임이 이보다 짧으면 믿을만한 스펙트럼을 얻을 수 있는 샘플이 충분하지 않으며, 프레임이 길면 프레임 전체에서 신호가 너무 많이 변경됩니다.

  
frame_size = 0.025
frame_stride = 0.01

frame_length, frame_step = frame_size * sample_rate, frame_stride * sample_rate
signal_length = len(emphasized_signal)
frame_length = int(round(frame_length))
frame_step = int(round(frame_step))
num_frames = int(np.ceil(float(np.abs(signal_length - frame_length)) / frame_step))

pad_signal_length = num_frames * frame_step + frame_length
z = np.zeros((pad_signal_length - signal_length))
pad_signal = np.append(emphasized_signal, z)

indices = np.tile(np.arange(0, frame_length), (num_frames, 1)) + np.tile(np.arange(0, num_frames * frame_step, frame_step), (frame_length, 1)).T
frames = pad_signal[indices.astype(np.int32, copy=False)]

print("Shape of Frames:", np.shape(frames))

    Shape of Frames: (328, 1200)

3. Window 함수 적용

Hamming Window 함수 적용

$w[x] = 0.54 - 0.46 \cos (\frac{w\pi n}{N-1})$ where $0<=n<=N-1,$ $\text{N is the window length.}$

  
frames *= np.hamming(frame_length)

FFT가 데이터가 무한하다고 가정하는 것을 보정하고 주파수 영역에서의 정보를 누출 (Leakage)을 줄입니다.

4. 각 프레임에 대해 Short-time Fourier Transform (STFT)를 수행하여 Power Spectrum을 계산합니다.

귀에 들어오는 소리의 주파수에 따라 다양한 지점에서 달팽이관이 진동하며, 진동하는 달팽이관의 위치에 따라 여러 신경이 활성화되어 특정 주파수가 있다는 사실을 뇌에 알립니다.
- Power Spectrum은 이와 유사한 작업을 수행하여 각 프레임에 어떤 주파수가 있는지 식별합니다.
고속 푸리에 변환 (FFT, Fast Fourier Transform)을 통해 음성 신호를 주파수 도메인으로 변환하여 스펙트럼을 얻을 수 있습니다.
각 프레임에 N-point FFT(Fast Fourier Transform) (=STFT) 를 수행하여 주파수 스펙트럼, 즉 Short-Time Fourier Transform (STFT)을 계산합니다.
- 음성을 작게 자른 조각에 푸리에 변환을 적용하는 느낌입니다.
N은 일반적으로 256, 512 값을 세팅합니다.
Power Spectrum (Periodogram)은 다음과 같이 계산됩니다.
- $P = \frac{| \text{FFT} (x_i) | ^2}{N}$

  
NFFT = 256
mag_frames = np.absolute(np.fft.rfft(frames, NFFT))  # Magnitude of the FFT
pow_frames = ((1.0 / NFFT) * ((mag_frames) ** 2))  # Power Spectrum

5. Power Spectrum을 Mel Scale에서의 Filter Bank로 변환합니다.

달팽이관은 밀접한 두 주파수 사이의 차이를 식별할 수 없기에, Power Spectrum에는 불필요한 정보가 많이 포함되어 있습니다.
- 따라서 Mel Filter Banck를 활용하여 Power Spectrum Bin들을 수집하여 합산하고, 각 주파수 영역에 얼마나 많은 에너지가 존재하는지를 분석합니다.
- 주파수가 높아질수록 Filter는 더 넓어지고 변화에 덜 민감해집니다.
Mel Spectrum은 사람의 청각 시스템이 높은 주파수보다 낮은 주파수 대역에서 민감하다는 특성을 반영하여 설계된 스펙트럼 표현 방법입니다.
- 이때 사용되는 Mel Scale 값은 물리적인 주파수와 사람이 인식하는 주파수 간의 관계를 나타내는 척도로 사용되며 Filter Bank의 간격과 너비를 정확하게 알려줍니다.
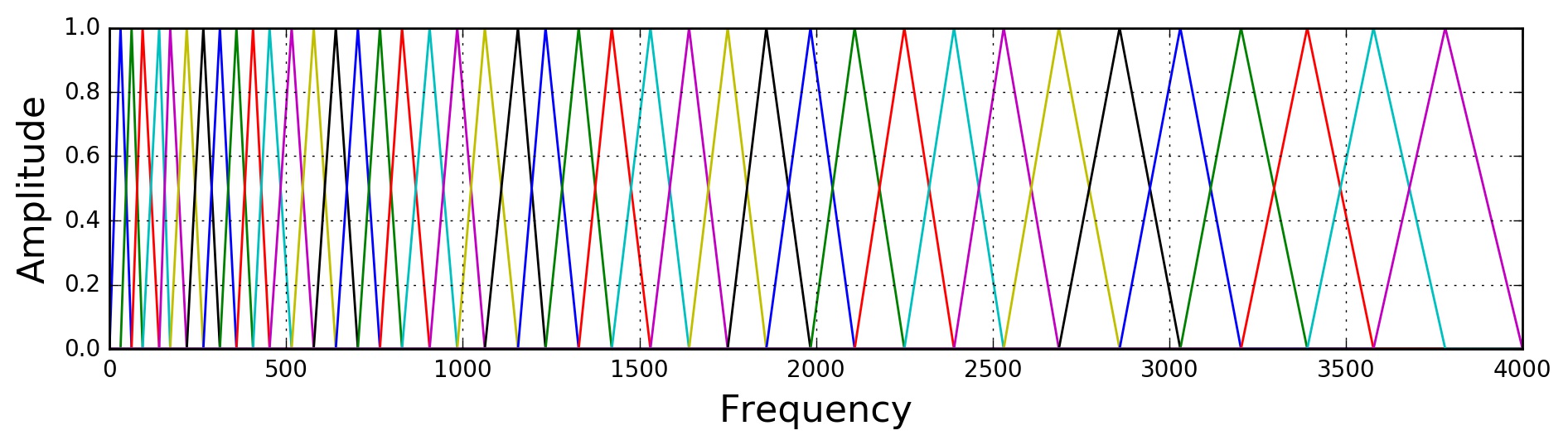
Filter Bank를 추출하기 위해 주로 Mel Scale에서 파생된 40개의 삼각형 필터를 Power Spectrum에 적용합니다.
헤르츠(Hertz, f)와 멜(Mel, m) 사이의 변환은 다음과 같은 방정식을 사용하여 수행할 수 있습니다:
- $m = 2595\log_{10}(a + \frac{f}{700})$
- $f = 700(10^{m/2595}-1)$
Filter Bank 내 각 필터는 삼각형 모형이며, 중심 주파수에서의 response가 1이고 주변 두 필터의 중심 주파수에 도달할 때 까지 선형적으로 감소하여 response가 0이 됩니다.

우리는 선형 규모의 소리를 듣지 못하기 때문에, 사람이 실제로 듣는 것과 밀접하게 로그를 취해줍니다.

  
nfilt = 40
low_freq_mel = 0
high_freq_mel = (2595 * np.log10(1 + (sample_rate / 2) / 700))  # Convert Hz to Mel
mel_points = np.linspace(low_freq_mel, high_freq_mel, nfilt + 2)  # Equally spaced in Mel scale
hz_points = (700 * (10**(mel_points / 2595) - 1))  # Convert Mel to Hz
bin = np.floor((NFFT + 1) * hz_points / sample_rate)

fbank = np.zeros((nfilt, int(np.floor(NFFT / 2 + 1))))
for m in range(1, nfilt + 1):
    f_m_minus = int(bin[m - 1])   # left
    f_m = int(bin[m])             # center
    f_m_plus = int(bin[m + 1])    # right

    for k in range(f_m_minus, f_m):
        fbank[m - 1, k] = (k - bin[m - 1]) / (bin[m] - bin[m - 1])
    for k in range(f_m, f_m_plus):
        fbank[m - 1, k] = (bin[m + 1] - k) / (bin[m + 1] - bin[m])
filter_banks = np.dot(pow_frames, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)  # Numerical Stability
filter_banks = 20 * np.log10(filter_banks)  # dB

6. Mean Normalization

Mel-scaled Filter Bank 특성을 원한다면 해당 과정은 스킵하셔도 됩니다.
스펙트럼을 균형있게 해주며 SNR을 향상시키기 위해 각 계수의 평균을 모든 프레임에서 빼는 계산을 수행합니다.

  
filter_banks -= (numpy.mean(filter_banks, axis=0) + 1e-8)

MFCC (Mel-Frequency Cepstral Coefficients)

1. 이전 단계에서 계산한 Filter Bank에 Discrete Cosine Transform (DCT)를 적용한 후 결과로 나온 계수들 중 일부만 보존합니다.

Filter Bank는 높은 상관관계를 가질 수 있는데 이는 머신러닝/딥러닝 알고리즘에 치명적입니다.
- 따라서, Filter Bank 계수의 상관관계를 제거하고 Filter Bank의 압축된 표현을 DCT를 통해 얻습니다.
- DCT는 에너지를 역상관시킵니다.
Cepstral 계수 중 2에서 13까지의 계수를 보존하고 나머지는 버립니다.
- 더 높은 DCT 계수가 Filter Bank 에너지의 빠른 변화를 나타내고 이는 모델링 (ASR)의 성능을 저하시킵니다.
- 주요 정보만을 보존하여 모델 성능을 향상시킬 수 있습니다.

  
num_ceps = 12
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)]  # Keep 2-13

2. MFCC내 큰 계수들을 강조하거나 무시하는 데 Sinusoidal Liftering을 적용할 수 있습니다.

노이즈가 있는 환경에서 더 정확한 음성 인식이 가능합니다.

  
cep_lifter = 22
(nframes, ncoeff) = mfcc.shape
n = np.arange(ncoeff)
lift = 1 + (cep_lifter / 2) * np.sin(np.pi * n / cep_lifter)
mfcc *= lift  #*

print("Shape of MFCCs:", np.shape(mfcc))

    Shape of MFCCs: (328, 12)

3. Mean Normalization

  
mfcc -= (np.mean(mfcc, axis=0) + 1e-8)

References

@misc{fayek2016,
title = “Speech Processing for Machine Learning: Filter banks, Mel-Frequency Cepstral Coefficients (MFCCs) and What’s In-Between”,
author = “Haytham M. Fayek”,
year = “2016”,
url = “https://haythamfayek.com/2016/04/21/speech-processing-for-machine-learning.html”
}
Speech Emotion Recognition
Mel Frequency Cepstral Coefficient (MFCC) tutorial, practicalcryptography.com/miscellaneous/machine-learning/guide-mel-frequency-cepstral-coefficients-mfccs/

AI Theory, Audio

This post is licensed under CC BY 4.0 by the author.